Lecture 9

An Introduction to Gaussian Processes

An introduction to Gaussian processes

A few remarks

• Gaussian process (GP) models assume that the vector of targets (e.g., \mathbf{t} ) come from a Gaussian distribution.

• Rather than opting for a parametric form of the regression function, in GPs a mean vector and a covariance matrix are selected for this Gaussian.

• Following Chapter 2 of Rasmussen and Williams, we shall begin with a noise-free case, followed by the noisy case.

• Notionally, with GPs, we assume that our function is an infinite dimensional Gaussian! However, any subset of this infinite dimensional Gaussian is by definition also Gaussian!

An introduction to Gaussian processes

GP prior

• Let \boldsymbol{x} \in \mathbb{R}^{d} denote a point in d-dimensional space, i.e., \boldsymbol{x} \in \mathcal{X}

• As with any Gaussian, a GP is typically specified through its mean \mu\left( \mathbf{x} \right) and a two-point covariance function k \left( \boldsymbol{x}, \boldsymbol{x}' \right).

• A popular choice for the mean function is \mu\left( \boldsymbol{x} \right) = 0 for all x \in \mathcal{X}.

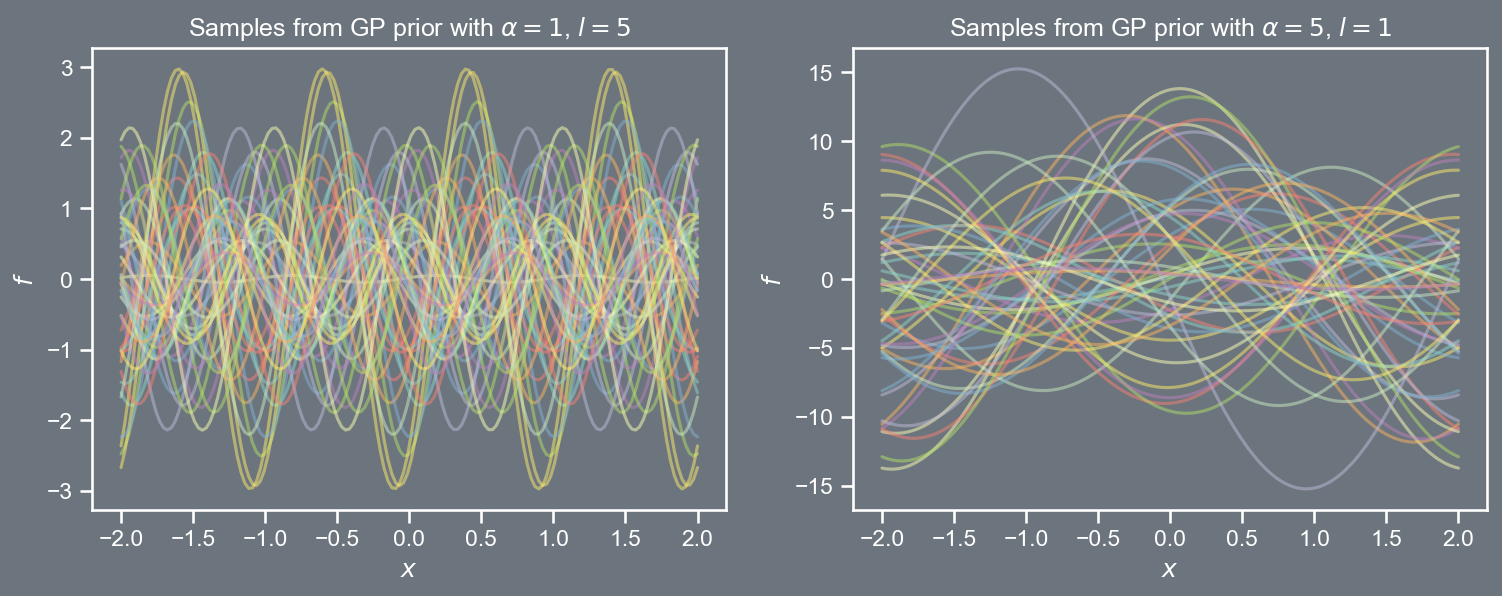
• Covariance functions are typically parameterized, and a popular choice is the radial basis function (also known as the squared exponential) k \left( \boldsymbol{x}, \boldsymbol{x}' \right) = \alpha \; exp \left(- \frac{1}{2l^2} \left\Vert \boldsymbol{x} - \boldsymbol{x}' \right\Vert_{2}^{2} \right) where l is the length scale and \alpha is the amplitude.

• The function k is referred to as the kernel function.

An introduction to Gaussian processes

Visualizing GP priors

• Plot
• Code

Defining a grid of points \mathcal{X} \equiv \left[-2, 2 \right], and choosing values for \alpha and l, we can sample vectors \mathbf{t} from the GP prior \mathcal{N}\left(\mathbf{0}, \mathbf{C} \right), where \mathbf{C}_{ij} = k \left( \boldsymbol{x}_{i}, \boldsymbol{x}_{j} \right).

import pandas as pd
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
from scipy.linalg import cholesky, solve_triangular
import seaborn as sns
sns.set(font_scale=1.0)
sns.set_style("white")
sns.set_style("ticks")
palette = sns.color_palette('deep')
plt.style.use('dark_background')


def kernel(xa, xb, amp, ll):
    Xa, Xb = get_tiled(xa, xb)
    return amp**2 * np.exp(-0.5 * 1./ll**2 * (Xa - Xb)**2 )


def get_tiled(xa, xb):
    m, n = len(xa), len(xb)
    xa, xb = xa.reshape(m,1) , xb.reshape(n,1)
    Xa = np.tile(xa, (1, n))
    Xb = np.tile(xb.T, (m, 1))
    return Xa, Xb

X = np.linspace(-2, 2, 150)
cov_1 = kernel(X, X, 1, 0.1) 
mu_1 = np.zeros((150,))
prior_1 = multivariate_normal(mu_1, cov_1, allow_singular=True)

cov_2 = kernel(X, X, 0.5, 1)
mu_2 = np.zeros((150,))
prior_2 = multivariate_normal(mu_2, cov_2, allow_singular=True)

random_samples = 50

fig, ax = plt.subplots(2, figsize=(12,4))
fig.patch.set_facecolor('#6C757D')
ax[0].set_fc('#6C757D')
plt.subplot(121)
plt.plot(X, prior_1.rvs(random_samples).T, alpha=0.5)
plt.title(r'Samples from GP prior with $\alpha=1$, $l=0.1$')
plt.xlabel(r'$x$')
plt.ylabel(r'$f$')
#plt.ylabel(r'$\mathbf{w}_1$')
fig.patch.set_facecolor('#6C757D')

plt.subplot(122)
plt.rcParams['axes.facecolor']='#6C757D'
ax[1].set_facecolor('#6C757D')
plt.plot(X, prior_2.rvs(random_samples).T, alpha=0.5)
plt.title(r'Samples from GP prior with $\alpha=0.5$, $l=1$')
plt.xlabel(r'$x$')
plt.ylabel(r'$f$')
plt.savefig('prior.png', dpi=150, bbox_inches='tight', facecolor="#6C757D")
plt.close()

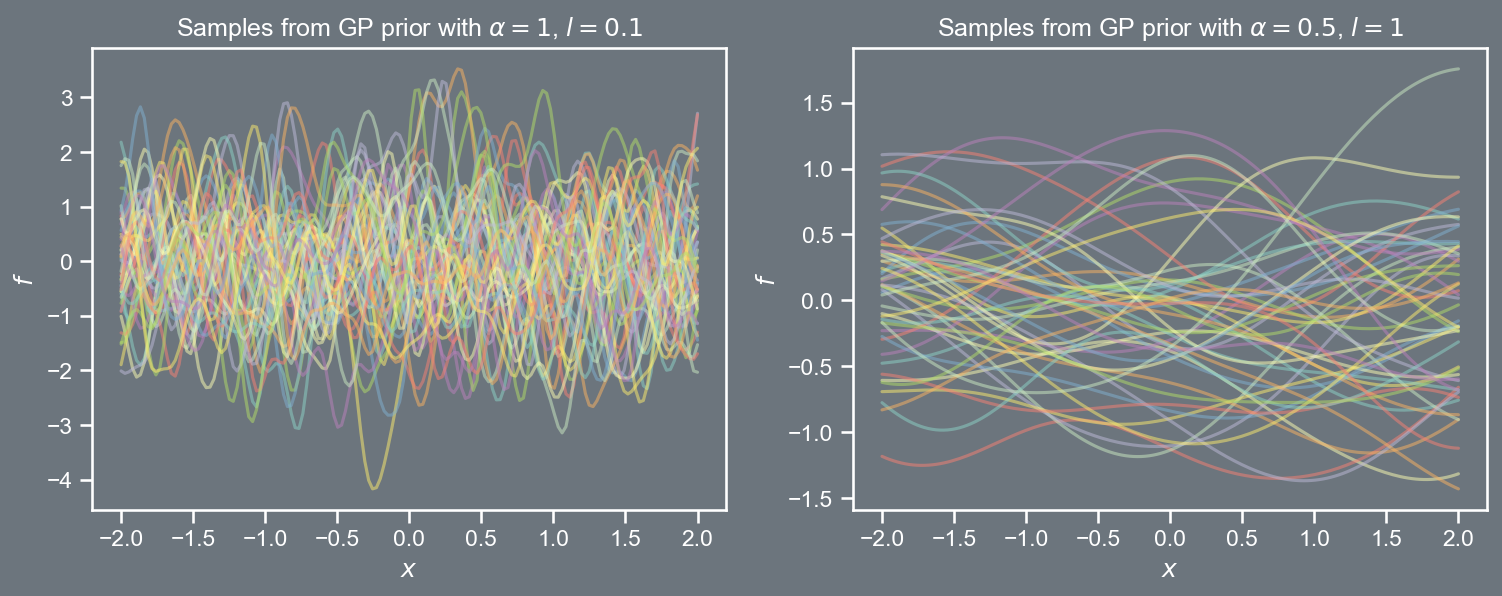
An introduction to Gaussian processes

Visualizing GP priors

• The prior covariance function depended only on the difference between pairs of points, i.e., \left\Vert \boldsymbol{x} - \boldsymbol{x}' \right\Vert_{2}^{2}.

• Such kernels are said to be stationary; an RBF kernel can be written as

k \left( \boldsymbol{r} \right) = \alpha \; exp \left(- \frac{1}{2l^2} \boldsymbol{r}^2 \right).

• We will encounter many kernel functions later on, some of them are stationary, whilst others are not.

An introduction to Gaussian processes

Gaussian marginals and conditionals

Click here.

An introduction to Gaussian processes

Noise-free regression

• We will consider the Olympic winning times dataset again, but this time assume there is no observational sensor noise.

• The markers denote the training \left(x_i, f_i \right) pairs, while the dashed lines denote the locations are which we would like to make predictions. we will use the superscript \ast to denote points at which we would like to infer predictions \underbrace{\mathbf{x}=\left[\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_N \\ \end{array}\right], \; \;\; \mathbf{f}=\left[\begin{array}{c} f_1\\ f_2\\ \vdots \\ f_N \\ \end{array}\right]}_{\text{training}}, \; \; \; \; \; \; \underbrace{\mathbf{x}^{\ast}=\left[\begin{array}{c} x_1^{\ast} \\ x_2^{\ast} \\ \vdots \\ x_L^{\ast} \\ \end{array}\right], \; \;\; \mathbf{f}^{\ast}=\left[\begin{array}{c} f_1^{\ast}\\ f_2^{\ast}\\ \vdots \\ f_L^{\ast} \\ \end{array}\right]}_{\text{prediction}} where N denotes the number of points in the training set, and L denotes the number of points in the prediction set.

• It will be useful to combine the winning times (both training and prediction) in the same vector, i.e., \mathbf{\hat{f}} = \left[ \mathbf{f}, \mathbf{f}^{\ast} \right]^{T}.

An introduction to Gaussian processes

Noise-free regression

It will be useful to define three covariance matrices:

1. A covariance matrix, \mathbf{C} \in \mathbb{R}^{N\times N}, on the training data: \mathbf{C}=\left[\begin{array}{ccc} k\left(x_{1},x_{1}\right) & \ldots & k\left(x_{1},x_{N}\right)\\ \vdots & \ddots & \vdots\\ k\left(x_{N},x_{1}\right) & \cdots & k\left(x_{N},x_{N}\right) \end{array}\right]

2. A covariance matrix, \mathbf{C}^{\ast} \in \mathbb{R}^{L\times L}, on the prediction (or test) data: \mathbf{C}^{\ast}=\left[\begin{array}{ccc} k\left(x_{1}^{\ast},x_{1}^{\ast}\right) & \ldots & k\left(x_{1}^{\ast},x_{L}^{\ast}\right)\\ \vdots & \ddots & \vdots\\ k\left(x_{L}^{\ast},x_{1}^{\ast}\right) & \cdots & k\left(x_{L}^{\ast},x_{L}^{\ast}\right) \end{array}\right]

3. A cross-covariance matrix, \mathbf{R} \in \mathbb{R}^{N \times L} on the training and testing data: \mathbf{R} = \left[\begin{array}{ccc} k\left(x_{1},x_{1}^{\ast}\right) & \ldots & k\left(x_{1},x_{L}^{\ast}\right)\\ \vdots & \ddots & \vdots\\ k\left(x_{N},x_{1}^{\ast}\right) & \cdots & k\left(x_{N},x_{L}^{\ast}\right) \end{array}\right]

An introduction to Gaussian processes

Noise-free regression

• Assuming a zero mean, the GP prior over \hat{\mathbf{t}} is given by p \left( \mathbf{\hat{f}} \right) = \mathcal{N} \left( \mathbf{0}, \left[\begin{array}{cc} \mathbf{C} & \mathbf{R} \\ \mathbf{R}^{T} & \mathbf{C}^{\ast} \end{array}\right] \right)

• This distribution is the complete definition of our model. It tells us how the function values at the training and prediction points co-vary.

• Making predictions amounts to manipulating this distribution to give a distribution over the function values at the prediction points conditioned on the observed training data, i.e., p \left( \mathbf{t}^{\ast} | \mathbf{t} \right)

• From our prior foray into Gaussian conditionals, we recognize this to be \begin{aligned} p \left( \mathbf{f}^{\ast} | \mathbf{f} \right) & = \mathcal{N}\left( \boldsymbol{\mu}^{\ast}, \boldsymbol{\Sigma}^{\ast} \right), \; \; \; \; \text{where} \\ \boldsymbol{\mu}^{\ast} = \mathbf{R}^{T} \mathbf{C}^{-1} \mathbf{f}, \; \; & \; \; \boldsymbol{\Sigma}^{\ast} = \mathbf{C}^{\ast} - \mathbf{R}^{T} \mathbf{C}^{-1} \mathbf{R} \end{aligned}

An introduction to Gaussian processes

Visualizing GP posteriors

• Plot
• Code

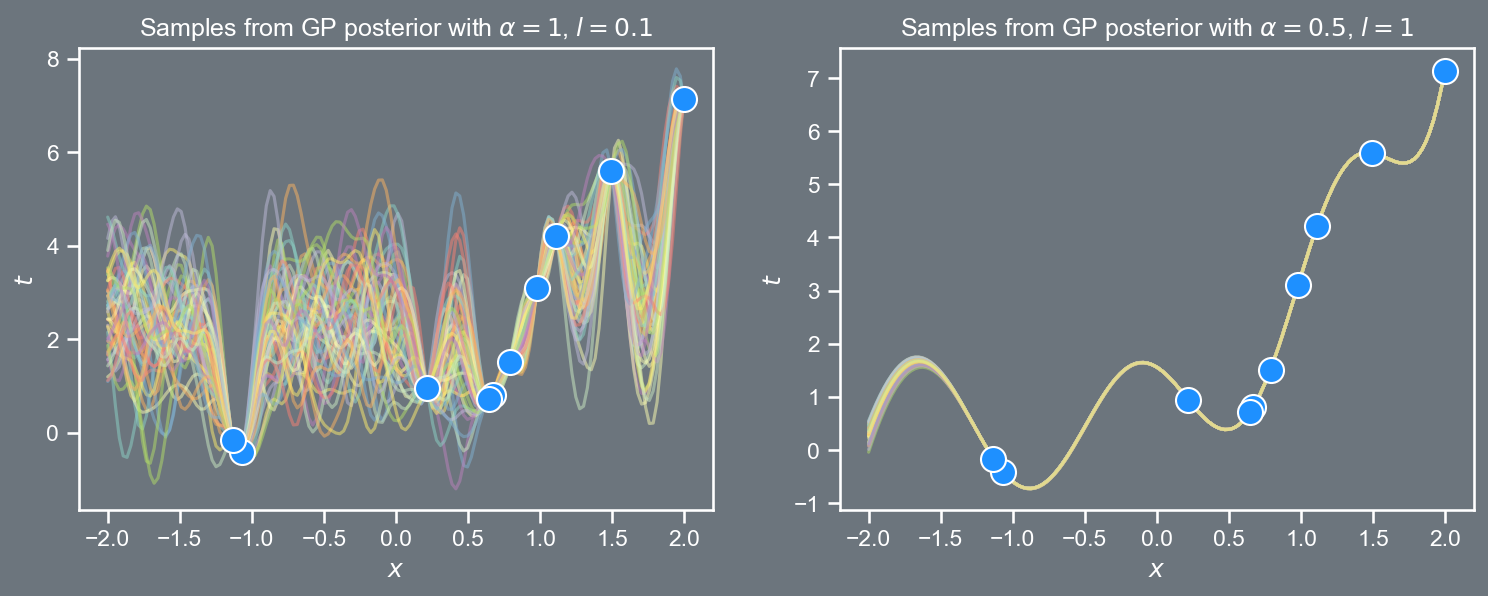
import pandas as pd
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
from scipy.linalg import cholesky, solve_triangular
import seaborn as sns
sns.set(font_scale=1.0)
sns.set_style("white")
sns.set_style("ticks")
palette = sns.color_palette('deep')
plt.style.use('dark_background')


def kernel(xa, xb, amp, ll):
    Xa, Xb = get_tiled(xa, xb)
    return amp**2 * np.exp(-0.5 * 1./ll**2 * (Xa - Xb)**2 )

def get_tiled(xa, xb):
    m, n = len(xa), len(xb)
    xa, xb = xa.reshape(m,1) , xb.reshape(n,1)
    Xa = np.tile(xa, (1, n))
    Xb = np.tile(xb.T, (m, 1))
    return Xa, Xb

def get_posterior(amp, ll, x, x_data, y_data):
    u = y_data.shape[0]
    mu_y = np.mean(y_data)
    y = (y_data - mu_y).reshape(u,1)
    
    Kxx = kernel(x_data, x_data, amp, ll)
    Kxpx = kernel(x, x_data, amp, ll)
    Kxpxp = kernel(x, x, amp, ll)
    
    # Inverse
    jitter = np.eye(u) * 1e-8
    L = cholesky(Kxx + jitter)
    S1 = solve_triangular(L.T, y, lower=True)
    S2 = solve_triangular(L.T, Kxpx.T, lower=True).T
    
    mu = S2 @ S1  + mu_y
    cov = Kxpxp - S2 @ S2.T
    return mu, cov

x_data = np.random.rand(10)*4 - 2.
y_data = np.cos(5*x_data) + x_data**2 + 2*x_data
X = np.linspace(-2, 2, 150)
random_samples = 50

fig, ax = plt.subplots(2, figsize=(12,4))
fig.patch.set_facecolor('#6C757D')
ax[0].set_fc('#6C757D')
plt.subplot(121)
mu, cov = get_posterior(1, 0.1, X, x_data, y_data)
posterior = multivariate_normal(mu.flatten(), cov, allow_singular=True)
#mu = mu.flatten()
#std = np.sqrt(np.diag(cov)).flatten()
plt.plot(x_data, y_data, 'o', ms=12, color='dodgerblue', lw=1, markeredgecolor='w', zorder=3)
plt.plot(X, posterior.rvs(random_samples).T, alpha=0.5, zorder=2)
plt.title(r'Samples from GP posterior with $\alpha=1$, $l=0.1$')
plt.xlabel(r'$x$')
plt.ylabel(r'$t$')
#plt.ylabel(r'$\mathbf{w}_1$')
fig.patch.set_facecolor('#6C757D')

plt.subplot(122)
plt.rcParams['axes.facecolor']='#6C757D'
ax[1].set_facecolor('#6C757D')
mu2, cov2 = get_posterior(0.5, 1, X, x_data, y_data)
posterior2 = multivariate_normal(mu2.flatten(), cov2, allow_singular=True)
plt.plot(x_data, y_data, 'o', ms=12, color='dodgerblue', lw=1, markeredgecolor='w', zorder=3)
plt.plot(X, posterior2.rvs(random_samples).T, alpha=0.5, zorder=2)
plt.title(r'Samples from GP posterior with $\alpha=0.5$, $l=1$')
plt.xlabel(r'$x$')
plt.ylabel(r'$t$')
plt.savefig('posterior.png', dpi=150, bbox_inches='tight', facecolor="#6C757D")
plt.close()

An introduction to Gaussian processes

Kernel functions

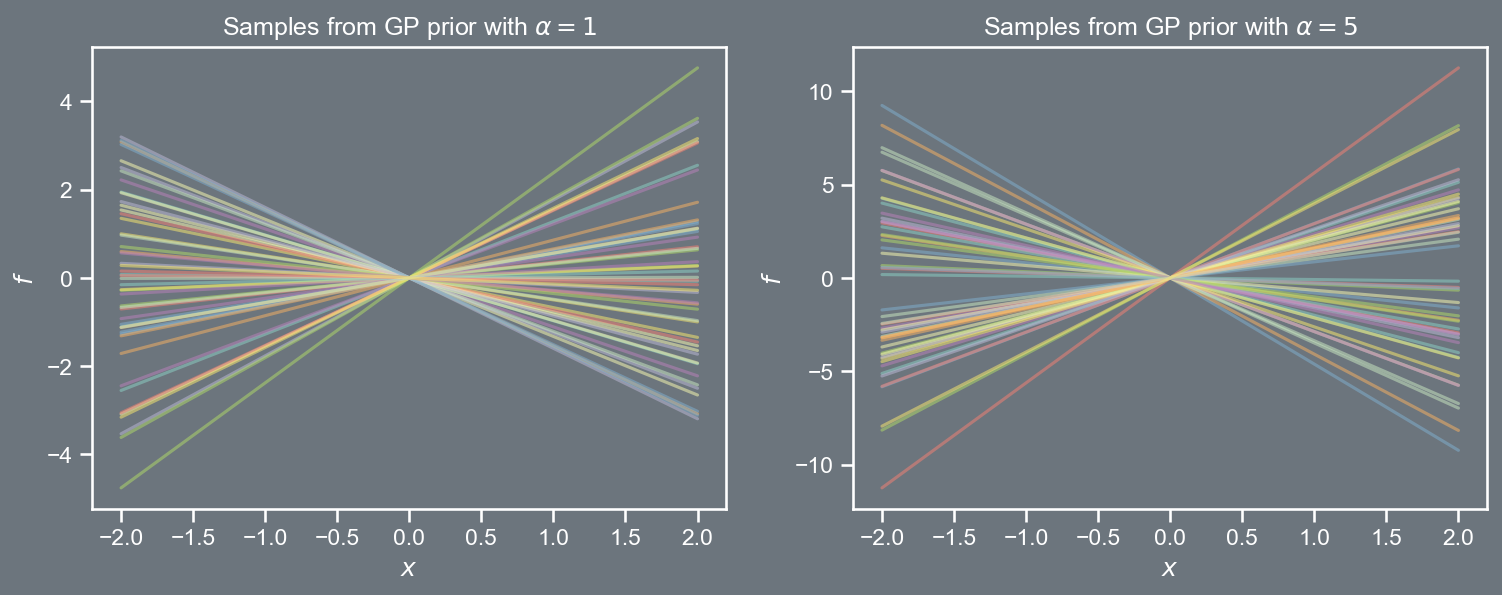
The RBF covariance function presented in the prior section is not the only candidate for a kernel function. Consider some of the other ones.

• Linear
• Polynomial
• Cosine

k \left( \boldsymbol{x}, \boldsymbol{x}' \right) = \alpha \; \boldsymbol{x}^{T} \boldsymbol{x}'

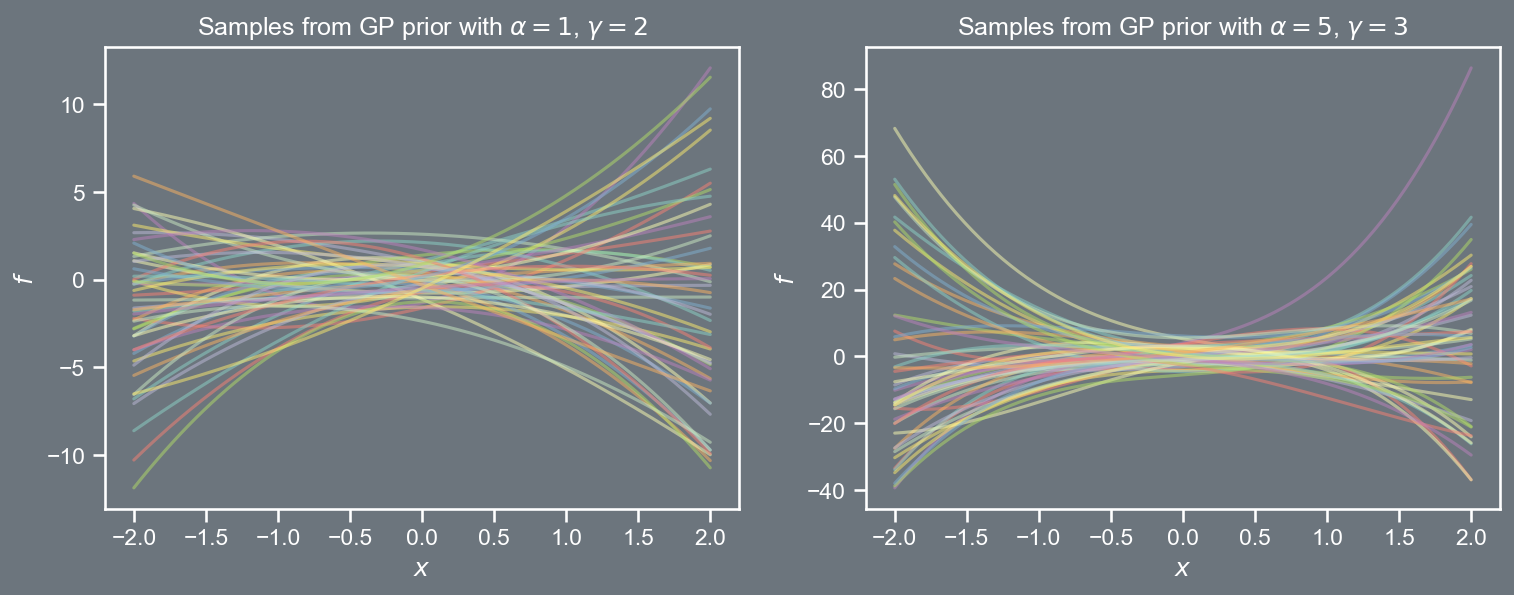
k \left( \boldsymbol{x}, \boldsymbol{x}' \right) = \alpha \; \left( 1 + \boldsymbol{x}^{T} \boldsymbol{x}' \right)^{\gamma}

k \left( \boldsymbol{x}, \boldsymbol{x}' \right) = \alpha^2 \; cos\left( \frac{2 \pi}{l^2} \left\Vert \boldsymbol{x} - \boldsymbol{x}' \right\Vert_{2}^{2} \right)