Thermodynamics

Problem 1

Carbon dioxide (with a molar mass of \(44 \; g/mol\)) behaves like a semi-perfect gas at moderate pressures and temperatures. Over the temperature range \(\require{color}{\color[rgb]{0.164799,0.878862,0.723179}500^{\circ} \; C}\) to \(\require{color}{\color[rgb]{0.164799,0.878862,0.723179}1200^{\circ} \; C}\), its constant volume specific heat capacity is accurately represented by the linear relation:

\[ \large \require{color} {\color[rgb]{0.878548,0.880173,0.060757}c}_{\color[rgb]{0.079785,0.618358,0.483717}V} = \alpha + \beta {\color[rgb]{0.164799,0.878862,0.723179}T} \]

where \(\alpha=555.65 \; J / \left( kg \cdot K \right)\) and \(\beta = 0.392 \; J / \left( kg \cdot K^2 \right)\). Please note that in the expression above \(\require{color}{\color[rgb]{0.164799,0.878862,0.723179}T}\) is in units Kelvin. A quantity of carbon dioxide undergoes a fully resisted expansion in an insulated cylinder. The initial pressure, volume, and temperature are \({\color[rgb]{0.315209,0.728565,0.037706}0.3 \; MPa}\), \({\color[rgb]{0.079785,0.618358,0.483717}0.1 \; m^3}\) and \({\color[rgb]{0.164799,0.878862,0.723179}950^{\circ} \; C}\) respectively. At the end of the expansion the temperature has fallen to \({\color[rgb]{0.164799,0.878862,0.723179}600^{\circ} \; C}\). You will need the universal gas constant value of \(8.3145 \; J / \left( mol \cdot K \right)\).

  1. Calculate the mass of carbon dioxide in the cylinder.

  2. Is the relationship \(\require{color}{\color[rgb]{0.315209,0.728565,0.037706}p}{\color[rgb]{0.079785,0.618358,0.483717}V}^{\gamma} = constant\) valid for this process?

  3. Calculate the final volume and pressure.

  4. Determine the work done during the expansion.

Solution
  1. The mass is given by

\[ \large \require{color} m = \frac{{\color[rgb]{0.315209,0.728565,0.037706}p}V}{ R{\color[rgb]{0.164799,0.878862,0.723179}T}} \]

where for carbon dioxide we have

\[ \large R = \frac{8.3145 \; \frac{J}{mol \cdot K}}{44 \; \frac{g}{mol}} = 0.18896 \frac{J}{g \cdot K} \times \frac{1000 \; g }{kg} = 189 \frac{J}{kg \cdot K}. \]

Please note that for both perfect and semi-perfect gases, the ideal gas equation is valid. Thus the mass is given by

\[ \large \require{color} m = {\color[rgb]{0.315209,0.728565,0.037706}0.3 \times 10^6} \times \frac{{\color[rgb]{0.079785,0.618358,0.483717}0.1}}{189 \times \left({\color[rgb]{0.164799,0.878862,0.723179} 950 + 273.15}\right) }=0.130 \; kg \]

  1. No the relationship is not constant because this is not a perfect gas (where \(\require{color}{\color[rgb]{0.878548,0.880173,0.060757}c}_{\color[rgb]{0.079785,0.618358,0.483717}V}\) is a constant).

  2. The first law per unit mass (using specific quantities) is given by

\[ \large \require{color} {\color[rgb]{0.334690,0.296180,0.998454}dq} - {\color[rgb]{0.562040,0.190215,0.568721}dw} = {\color[rgb]{0.878548,0.880173,0.060757}du} \]

As the cylinder is given to be fully insulated, we assume an adiabatic process, i.e., \(\require{color}{\color[rgb]{0.334690,0.296180,0.998454}dq} = 0\). Additionally as its fully resisted, we have

\[ \large \require{color} {\color[rgb]{0.562040,0.190215,0.568721}dw} = {\color[rgb]{0.315209,0.728565,0.037706}p} {\color[rgb]{0.918231,0.469102,0.038229}d \nu} \]

where \(\require{color}{\color[rgb]{0.918231,0.469102,0.038229}\nu}\) is the specific volume. From these relationships we arrive at

\[ \large \require{color} {\color[rgb]{0.315209,0.728565,0.037706}p} {\color[rgb]{0.918231,0.469102,0.038229}d \nu} + {\color[rgb]{0.878548,0.880173,0.060757}du} = 0 \]

Recognizing that the internal energy is specific and using the definition of an ideal gas we have

\[ \large \require{color} R{\color[rgb]{0.164799,0.878862,0.723179}T}\frac{{\color[rgb]{0.918231,0.469102,0.038229}d\nu}}{{\color[rgb]{0.918231,0.469102,0.038229}\nu}} + {\color[rgb]{0.878548,0.880173,0.060757}c}_{{\color[rgb]{0.079785,0.618358,0.483717}V}} {\color[rgb]{0.164799,0.878862,0.723179}dT} = 0 \]

\[ \large \require{color} \Rightarrow R{\color[rgb]{0.164799,0.878862,0.723179}T}\frac{{\color[rgb]{0.918231,0.469102,0.038229}d\nu}}{{\color[rgb]{0.918231,0.469102,0.038229}\nu}} + \left( \alpha + \beta {\color[rgb]{0.164799,0.878862,0.723179}T} \right) {\color[rgb]{0.164799,0.878862,0.723179}dT} = 0 \]

\[ \large \require{color} \Rightarrow R{\color[rgb]{0.164799,0.878862,0.723179}T}\frac{{\color[rgb]{0.918231,0.469102,0.038229}d\nu}}{{\color[rgb]{0.918231,0.469102,0.038229}\nu}} + \alpha {\color[rgb]{0.164799,0.878862,0.723179}dT}+ \beta {\color[rgb]{0.164799,0.878862,0.723179}T} {\color[rgb]{0.164799,0.878862,0.723179}dT} = 0 \]

\[ \large \require{color} \Rightarrow R \frac{{\color[rgb]{0.918231,0.469102,0.038229}d\nu}}{{\color[rgb]{0.918231,0.469102,0.038229}\nu}} + \frac{\alpha}{{\color[rgb]{0.164799,0.878862,0.723179}T}} {\color[rgb]{0.164799,0.878862,0.723179}dT}+ \beta {\color[rgb]{0.164799,0.878862,0.723179}dT} = 0 \]

Now integrating between states 1 and 2 yields

\[ \large \require{color} R \; ln \left( \frac{{\color[rgb]{0.918231,0.469102,0.038229}\nu_2}}{{\color[rgb]{0.918231,0.469102,0.038229}\nu_1}} \right) = \alpha \; ln \left( \frac{{\color[rgb]{0.164799,0.878862,0.723179}T_1}}{{\color[rgb]{0.164799,0.878862,0.723179}T_2}} \right) + \beta \left({\color[rgb]{0.164799,0.878862,0.723179}T_1} - {\color[rgb]{0.164799,0.878862,0.723179}T_2} \right) \]

\[ \large \require{color} \Rightarrow ln \left( \frac{{\color[rgb]{0.079785,0.618358,0.483717}V_2}}{{\color[rgb]{0.079785,0.618358,0.483717}V_1}} \right) = ln \left( \frac{{\color[rgb]{0.918231,0.469102,0.038229}\nu_2}}{{\color[rgb]{0.918231,0.469102,0.038229}\nu_1}} \right) = \frac{\alpha}{R} ln \left( \frac{{\color[rgb]{0.164799,0.878862,0.723179}T_1}}{{\color[rgb]{0.164799,0.878862,0.723179}T_2}} \right) + \frac{\beta}{R} \left({\color[rgb]{0.164799,0.878862,0.723179}T_1} - {\color[rgb]{0.164799,0.878862,0.723179}T_2} \right) \]

\[ \large \require{color} = \frac{555.65}{189} \; ln \left(\frac{{\color[rgb]{0.164799,0.878862,0.723179}1223.15}}{{\color[rgb]{0.164799,0.878862,0.723179}873.15}} \right) + \frac{0.392}{189} \left({\color[rgb]{0.164799,0.878862,0.723179}1223.15} - {\color[rgb]{0.164799,0.878862,0.723179}873.15} \right) \]

This leads to

\[ \large \require{color} {\color[rgb]{0.079785,0.618358,0.483717}V_2} = 5.567 {\color[rgb]{0.079785,0.618358,0.483717}V_1} \Rightarrow {\color[rgb]{0.079785,0.618358,0.483717}V_2} = {\color[rgb]{0.079785,0.618358,0.483717}0.557 \; m^3} \]

Now we can work out the final pressure, i.e.,

\[ \large \require{color} {\color[rgb]{0.315209,0.728565,0.037706}p_2} = \frac{mR{\color[rgb]{0.164799,0.878862,0.723179}T_2}}{{\color[rgb]{0.079785,0.618358,0.483717}V_2}} = \frac{0.130 \times 189 \times {\color[rgb]{0.164799,0.878862,0.723179}873.15}}{{\color[rgb]{0.079785,0.618358,0.483717}0.557}} = {\color[rgb]{0.315209,0.728565,0.037706}38.50 \; kPa} \]

  1. The work done during the expansion is given by

\[ \require{color} \large {\color[rgb]{0.562040,0.190215,0.568721}W }= -{\color[rgb]{0.878548,0.880173,0.060757}\Delta U} = - m \int_{1}^{2} {\color[rgb]{0.878548,0.880173,0.060757}c}_{\color[rgb]{0.079785,0.618358,0.483717}V} {\color[rgb]{0.164799,0.878862,0.723179}dT} = m \int_{2}^{1} {\color[rgb]{0.878548,0.880173,0.060757}c}_{\color[rgb]{0.079785,0.618358,0.483717}V} {\color[rgb]{0.164799,0.878862,0.723179}dT} = m \left[ \alpha \left( {\color[rgb]{0.164799,0.878862,0.723179}T_1} - {\color[rgb]{0.164799,0.878862,0.723179}T_2} \right) + \frac{1}{2} \beta \left( {\color[rgb]{0.164799,0.878862,0.723179}T_1}^2 - {\color[rgb]{0.164799,0.878862,0.723179}T_2}^2 \right) \right]. \]

The numerical solution is given below

Code 
import numpy as np

m = 0.130
T_2 = 600 + 273.15
T_1 = 950 + 273.15
alpha = 555.65
beta = 0.392

W = m * (alpha * (T_1 - T_2) + 0.5 * beta * (T_1**2 - T_2**2))
print('Work done is '+str(np.round(W/1000, 3))+' kJ')
Work done is 43.977 kJ

Problem 2

A quantity of argon gas with \(\gamma = 1.67\), initially at \(\require{color}{\color[rgb]{0.315209,0.728565,0.037706}1 \; bar}\) and \(\require{color}{\color[rgb]{0.164799,0.878862,0.723179}300 \; K}\) is compressed adiabatically and reversibly (and hence isentropically) to half its initial volume. Calculate the final pressure and temperature.

Solution

As the question states, the process is isentropic. We can make use of the isentropic relations presented in Lecture 14, i.e.,

\[ \large \require{color} \frac{{\color[rgb]{0.315209,0.728565,0.037706}p_2}}{{\color[rgb]{0.315209,0.728565,0.037706}p_1}} = \left( \frac{{\color[rgb]{0.164799,0.878862,0.723179}V_1}}{{\color[rgb]{0.164799,0.878862,0.723179}V_2}} \right)^{\gamma} \Rightarrow {\color[rgb]{0.315209,0.728565,0.037706}p_2} = {\color[rgb]{0.315209,0.728565,0.037706}p_1} \left( \frac{{\color[rgb]{0.164799,0.878862,0.723179}V_1}}{{\color[rgb]{0.164799,0.878862,0.723179}V_2}} \right)^{\gamma} = {\color[rgb]{0.315209,0.728565,0.037706}1} \times {\color[rgb]{0.079785,0.618358,0.483717}2}^{1.67} = {\color[rgb]{0.315209,0.728565,0.037706}3.18 \; bar} \]

and for the temperature, we have

\[ \large \require{color} {\color[rgb]{0.164799,0.878862,0.723179}T_2} = {\color[rgb]{0.164799,0.878862,0.723179}T_1} \left( \frac{{\color[rgb]{0.079785,0.618358,0.483717}V_1}}{{\color[rgb]{0.079785,0.618358,0.483717}V_2}} \right)^{\gamma - 1} = {\color[rgb]{0.164799,0.878862,0.723179}300} \times {\color[rgb]{0.079785,0.618358,0.483717}2}^{0.67} = {\color[rgb]{0.164799,0.878862,0.723179}477.3 \; K} \]

Problem 3

A polytropic process is defined by the relation

\[ \large \require{color}{\color[rgb]{0.315209,0.728565,0.037706}p}{\color[rgb]{0.079785,0.618358,0.483717}V}^{n} = k \]

where \(n\) and \(k\) are constants.

  1. Show that for a fully resisted (i.e. quasi-equilibrium) polytropic expansion or compression of a gas between states 1 and 2, the displacement work done by the gas is given by

\[ \large \require{color}{\color[rgb]{0.562040,0.190215,0.568721}W} = \frac{{\color[rgb]{0.315209,0.728565,0.037706}p_1} {\color[rgb]{0.079785,0.618358,0.483717}V_1} - {\color[rgb]{0.315209,0.728565,0.037706}p_2} {\color[rgb]{0.079785,0.618358,0.483717}V_2}}{n-1} \]

provided \(1 \neq n\).

  1. Hence show that for a perfect gas undergoing a polytropic process, the ratio of heat to work transfer is:

\[ \large \require{color}\frac{{\color[rgb]{0.334690,0.296180,0.998454}Q}}{{\color[rgb]{0.562040,0.190215,0.568721}W}} = \frac{\gamma - n}{\gamma - 1} \]

  1. Use the result of b. to suggest how the value of \(n\) is likely to vary with the rate at which the process is undertaken. What happens to \(\require{color}{\color[rgb]{0.334690,0.296180,0.998454}Q}\) and \(\require{color}{\color[rgb]{0.562040,0.190215,0.568721}W}\) in the case of an extremely rapid expansion?
Solution
  1. The displacement work is given by

\[ \large \require{color} {\color[rgb]{0.562040,0.190215,0.568721}W} = \int {\color[rgb]{0.315209,0.728565,0.037706}p} \; {\color[rgb]{0.079785,0.618358,0.483717}dV} = \int_{1}^{2} \frac{k}{{\color[rgb]{0.079785,0.618358,0.483717}V}^n} {\color[rgb]{0.079785,0.618358,0.483717}dV} = k \left[ \frac{{\color[rgb]{0.079785,0.618358,0.483717}V}^{1-n}}{1-n} \right]_{1}^{2} = \frac{{\color[rgb]{0.315209,0.728565,0.037706}p_1} {\color[rgb]{0.079785,0.618358,0.483717}V_1} - {\color[rgb]{0.315209,0.728565,0.037706}p_2} {\color[rgb]{0.079785,0.618358,0.483717}V_2}}{n-1} \]

since \(\require{color}k = {\color[rgb]{0.315209,0.728565,0.037706}p_1} {\color[rgb]{0.079785,0.618358,0.483717}V_1}^{n} = {\color[rgb]{0.315209,0.728565,0.037706}p_2} {\color[rgb]{0.079785,0.618358,0.483717}V_2}^{n}\).

  1. For a perfect gas \(\require{color}{\color[rgb]{0.315209,0.728565,0.037706}p}V = mR{\color[rgb]{0.164799,0.878862,0.723179}T}\) and \(\require{color}{\color[rgb]{0.878548,0.880173,0.060757}\Delta U} = m {\color[rgb]{0.878548,0.880173,0.060757}c}_{\color[rgb]{0.079785,0.618358,0.483717}V} {\color[rgb]{0.164799,0.878862,0.723179}\Delta T}\), which results in

\[ \large \require{color} {\color[rgb]{0.562040,0.190215,0.568721}W} = \frac{{\color[rgb]{0.315209,0.728565,0.037706}p_1} {\color[rgb]{0.079785,0.618358,0.483717}V_1} - {\color[rgb]{0.315209,0.728565,0.037706}p_2} {\color[rgb]{0.079785,0.618358,0.483717}V_2}}{n-1} = mR \frac{\left({\color[rgb]{0.164799,0.878862,0.723179}T_1} - {\color[rgb]{0.164799,0.878862,0.723179}T_2}\right)}{n-1} \]

\[ \large \require{color} {\color[rgb]{0.878548,0.880173,0.060757}\Delta U} = m {\color[rgb]{0.878548,0.880173,0.060757}c}_{\color[rgb]{0.079785,0.618358,0.483717}V} \left({\color[rgb]{0.164799,0.878862,0.723179}T_2} - {\color[rgb]{0.164799,0.878862,0.723179}T_1} \right) = m R \frac{\left( {\color[rgb]{0.164799,0.878862,0.723179}T_2} - {\color[rgb]{0.164799,0.878862,0.723179}T_1} \right) }{\left(\gamma - 1\right) } \]

This yields

\[ \large \require{color} {\color[rgb]{0.334690,0.296180,0.998454}Q} = {\color[rgb]{0.878548,0.880173,0.060757}\Delta U} + {\color[rgb]{0.562040,0.190215,0.568721}W} = m R \left({\color[rgb]{0.164799,0.878862,0.723179}T_1} - {\color[rgb]{0.164799,0.878862,0.723179}T_2} \right) \left[ \frac{1}{n-1} - \frac{1}{\gamma - 1} \right] \]

Thus

\[ \large \require{color} \frac{{\color[rgb]{0.334690,0.296180,0.998454}Q}}{{\color[rgb]{0.562040,0.190215,0.568721}W}} = \left[ \frac{1}{n-1} - \frac{1}{\gamma-1} \right] \left(n - 1 \right) = \frac{\gamma - n}{\gamma - 1} \]

  1. For rapid processes, there is no time for heat transfer so \(\require{color}{\color[rgb]{0.334690,0.296180,0.998454}Q} = 0\) (adiabatic). Inspection of the above relation then shows \(n = γ\). For very slow processes the system remains in thermal equilibrium with the surroundings, so the process tends towards isothermal. Thus \[ \large \require{color} \frac{{\color[rgb]{0.334690,0.296180,0.998454}Q}}{{\color[rgb]{0.562040,0.190215,0.568721}W}} \rightarrow 1 \]
and hence \(n \rightarrow 1\). In the case of an extremely rapid expansion, the process is unresisted so no work will be extracted and there will be no time for heat transfer.

Problem 4

Starting from the first law of Thermodynamics and the definition of entropy

  1. show that for a reversible process

\[ \large \require{color} {\color[rgb]{0.164799,0.878862,0.723179}T} {\color[rgb]{0.599997,0.600015,0.600005}ds} = {\color[rgb]{0.878548,0.880173,0.060757}du} + {\color[rgb]{0.315209,0.728565,0.037706}p} {\color[rgb]{0.918231,0.469102,0.038229}d \nu} \]

  1. Furthermore, using the definition of enthalpy show that

\[ \large \require{color} {\color[rgb]{0.164799,0.878862,0.723179}T} {\color[rgb]{0.599997,0.600015,0.600005}ds} = {\color[rgb]{0.986252,0.007236,0.027423}dh} - {\color[rgb]{0.918231,0.469102,0.038229}\nu} {\color[rgb]{0.315209,0.728565,0.037706}dp} \]

  1. Hence show that for a perfect gas moving from a thermodynamic state 1 to another thermodynamic state 2

\[ \large \require{color} {\color[rgb]{0.599997,0.600015,0.600005}s_2} - {\color[rgb]{0.599997,0.600015,0.600005}s_1} = {\color[rgb]{0.986252,0.007236,0.027423}c}_{\color[rgb]{0.315209,0.728565,0.037706}p} \; ln \left( \frac{{\color[rgb]{0.164799,0.878862,0.723179}T_2}}{{\color[rgb]{0.164799,0.878862,0.723179}T_1}} \right) - R ln \left( \frac{{\color[rgb]{0.315209,0.728565,0.037706}p_2}}{{\color[rgb]{0.315209,0.728565,0.037706}p_1}} \right) \]

  1. Explain why the equation in (c) can be applied to an irreversible process.
Solution

Students, carefully note the various assumptions that are made below. Simply providing the equations is not sufficient; reasoning is key.

  1. From the first law of thermodynamics we have

\[ \large \require{color} {\color[rgb]{0.334690,0.296180,0.998454}Q} - {\color[rgb]{0.562040,0.190215,0.568721}W} = {\color[rgb]{0.878548,0.880173,0.060757}\Delta E} \]

where the contributions to energy are

\[ \large \require{color} {\color[rgb]{0.878548,0.880173,0.060757}\Delta E} = {\color[rgb]{0.878548,0.880173,0.060757}\Delta PE} + {\color[rgb]{0.878548,0.880173,0.060757}\Delta KE} + {\color[rgb]{0.878548,0.880173,0.060757}\Delta U} \]

Consider a simple compressible system undergoing an infinitesimal change of state by heat and work interactions with its surroundings. The first law then gives:

\[ \large \require{color} {\color[rgb]{0.334690,0.296180,0.998454}\delta Q }- {\color[rgb]{0.562040,0.190215,0.568721}\delta W} = {\color[rgb]{0.878548,0.880173,0.060757}dU} \]

From the definition of entropy,

\[ \large \require{color} {\color[rgb]{0.334690,0.296180,0.998454}\delta Q }= {\color[rgb]{0.164799,0.878862,0.723179}T}{\color[rgb]{0.599997,0.600015,0.600005}dS} \]

and for fully-resisted compression

\[ \large \require{color} {\color[rgb]{0.562040,0.190215,0.568721}\delta W} = {\color[rgb]{0.315209,0.728565,0.037706}p} {\color[rgb]{0.079785,0.618358,0.483717}dV} \]

so for a reversible process we have:

\[ \large \require{color} {\color[rgb]{0.164799,0.878862,0.723179}T}{\color[rgb]{0.599997,0.600015,0.600005}dS} - {\color[rgb]{0.315209,0.728565,0.037706}p}{\color[rgb]{0.079785,0.618358,0.483717}dV} = {\color[rgb]{0.878548,0.880173,0.060757}dU} \]

Now, dividing by the mass of the system and re-arranging we arrive at:

\[ \large \require{color} {\color[rgb]{0.164799,0.878862,0.723179}T}{\color[rgb]{0.599997,0.600015,0.600005}ds} = {\color[rgb]{0.878548,0.880173,0.060757}du} + {\color[rgb]{0.315209,0.728565,0.037706}p}{\color[rgb]{0.918231,0.469102,0.038229}d \nu} \]

  1. From the definition of enthalpy we have

\[ \large \require{color} {\color[rgb]{0.986252,0.007236,0.027423}h} = {\color[rgb]{0.878548,0.880173,0.060757}u} + {\color[rgb]{0.315209,0.728565,0.037706}p}{\color[rgb]{0.918231,0.469102,0.038229} \nu}. \]

Computing derivatives, we arrive at

\[ \large \require{color} {\color[rgb]{0.986252,0.007236,0.027423}dh} = {\color[rgb]{0.878548,0.880173,0.060757}du} + {\color[rgb]{0.315209,0.728565,0.037706}p}{\color[rgb]{0.918231,0.469102,0.038229}d\nu} {\color[rgb]{0.918231,0.469102,0.038229}\nu} {\color[rgb]{0.315209,0.728565,0.037706}dp} \]

\[ \large \require{color} \Rightarrow {\color[rgb]{0.878548,0.880173,0.060757}du} + {\color[rgb]{0.315209,0.728565,0.037706}p} {\color[rgb]{0.918231,0.469102,0.038229}d \nu} = {\color[rgb]{0.986252,0.007236,0.027423}dh} - {\color[rgb]{0.918231,0.469102,0.038229}\nu} {\color[rgb]{0.315209,0.728565,0.037706}dp} \]

\[ \large \require{color} \Rightarrow {\color[rgb]{0.164799,0.878862,0.723179}T}{\color[rgb]{0.599997,0.600015,0.600005}ds} = {\color[rgb]{0.986252,0.007236,0.027423}dh} - {\color[rgb]{0.918231,0.469102,0.038229}\nu} {\color[rgb]{0.315209,0.728565,0.037706}dp} \]

  1. For a perfect gas changing reversibly from state 1 to state 2, the above equations apply and also \(\require{color}{\color[rgb]{0.986252,0.007236,0.027423}c}_{\color[rgb]{0.315209,0.728565,0.037706}p}\) and \(\require{color}{\color[rgb]{0.878548,0.880173,0.060757}c}_{\color[rgb]{0.079785,0.618358,0.483717}V}\) are constant. This leads to

\[ \large \require{color} \int_{{\color[rgb]{0.599997,0.600015,0.600005}s_1}}^{{\color[rgb]{0.599997,0.600015,0.600005}s_2}} {\color[rgb]{0.599997,0.600015,0.600005}ds} = \int_{{\color[rgb]{0.986252,0.007236,0.027423}h_1}}^{{\color[rgb]{0.986252,0.007236,0.027423}h_2}} \frac{{\color[rgb]{0.986252,0.007236,0.027423}dh}}{{\color[rgb]{0.164799,0.878862,0.723179}T}} - \int_{{\color[rgb]{0.315209,0.728565,0.037706}p_1}}^{{\color[rgb]{0.315209,0.728565,0.037706}p_2}} \frac{{\color[rgb]{0.918231,0.469102,0.038229}\nu} {\color[rgb]{0.315209,0.728565,0.037706}dp}}{{\color[rgb]{0.164799,0.878862,0.723179}T}} \]

but by definition \(\require{color}{\color[rgb]{0.986252,0.007236,0.027423}dh} = {\color[rgb]{0.986252,0.007236,0.027423}c}_{\color[rgb]{0.315209,0.728565,0.037706}p} {\color[rgb]{0.164799,0.878862,0.723179}dT}\). Additionally, since the ideal gas relation holds for a perfect gas, we can re-write the above as

\[ \large \require{color} \int_{{\color[rgb]{0.599997,0.600015,0.600005}s_1}}^{{\color[rgb]{0.599997,0.600015,0.600005}s_2}} {\color[rgb]{0.599997,0.600015,0.600005}ds} = {\color[rgb]{0.986252,0.007236,0.027423}c}_{\color[rgb]{0.315209,0.728565,0.037706}p} \int_{{\color[rgb]{0.164799,0.878862,0.723179}T_1}}^{{\color[rgb]{0.164799,0.878862,0.723179}T_2}} \frac{{\color[rgb]{0.164799,0.878862,0.723179}dT}}{{\color[rgb]{0.164799,0.878862,0.723179}T}} - R \int_{{\color[rgb]{0.315209,0.728565,0.037706}p_1}}^{{\color[rgb]{0.315209,0.728565,0.037706}p_2}} \frac{{\color[rgb]{0.315209,0.728565,0.037706}dp}}{{\color[rgb]{0.315209,0.728565,0.037706}p}} \]

\[ \large \require{color} \Rightarrow {\color[rgb]{0.599997,0.600015,0.600005}s_2} - {\color[rgb]{0.599997,0.600015,0.600005}s_1} = {\color[rgb]{0.986252,0.007236,0.027423}c}_{\color[rgb]{0.315209,0.728565,0.037706}p} \; ln \left( \frac{{\color[rgb]{0.164799,0.878862,0.723179}T_2}}{{\color[rgb]{0.164799,0.878862,0.723179}T_1}} \right) - R ln \left( \frac{{\color[rgb]{0.315209,0.728565,0.037706}p_2}}{{\color[rgb]{0.315209,0.728565,0.037706}p_1}} \right) \]

  1. Because \(\require{color}{\color[rgb]{0.599997,0.600015,0.600005}S}, {\color[rgb]{0.164799,0.878862,0.723179}T}\) and \(\require{color}{\color[rgb]{0.315209,0.728565,0.037706}p}\) are thermodynamic properties, this relation also applies to irreversible processes.

Problem 5

Consider a closed system containing \(1 \; m^3\) of air at a pressure of \(\require{color}{\color[rgb]{0.315209,0.728565,0.037706}14.0 \; bar}\) and a temperature of \({\color[rgb]{0.164799,0.878862,0.723179}200^{\circ} \; C}\). The specific heat at consatnt volume may be taken as \({\color[rgb]{0.878548,0.880173,0.060757}c}_{\color[rgb]{0.079785,0.618358,0.483717}V} = {\color[rgb]{0.878548,0.880173,0.060757}0.74 \; kJ / (Kg \cdot K )}\). Please answer the queries below.

  1. What is the mass of the air in the system?

  2. If \(\require{color}{\color[rgb]{0.334690,0.296180,0.998454}1800 \; kJ}\) of heat is added to the system while its volume remains constant, what is the final pressure and temperature?

  3. If \(\require{color}{\color[rgb]{0.334690,0.296180,0.998454}1800 \; kJ}\) of heat is added to the system while its pressure remains constant, what is the final volume and temperature?

  4. Is there any process possible where the entropy of the system remains constant while receiving heat? Justify your answer.

Solution
  1. The mass of the air can be worked out using the equation of state

\[ \large \require{color} {\color[rgb]{0.315209,0.728565,0.037706}p}{\color[rgb]{0.079785,0.618358,0.483717}V} = m R{\color[rgb]{0.164799,0.878862,0.723179}T} \; \; \Rightarrow \; \; m = \frac{{\color[rgb]{0.315209,0.728565,0.037706}p}{\color[rgb]{0.079785,0.618358,0.483717}V}}{R{\color[rgb]{0.164799,0.878862,0.723179}T}} \]

\[ \large \require{color} m = \frac{14 \times 10^5 \times 1}{287 \times 473} = 10.313 \; kg \]

  1. From the first law, we have

\[ \large \require{color} {\color[rgb]{0.334690,0.296180,0.998454}Q} - {\color[rgb]{0.562040,0.190215,0.568721}W} = {\color[rgb]{0.878548,0.880173,0.060757}\Delta U} = m{\color[rgb]{0.878548,0.880173,0.060757}c}_{{\color[rgb]{0.079785,0.618358,0.483717}V}} {\color[rgb]{0.164799,0.878862,0.723179}\Delta T} \]

where we note that \(\require{color}{\color[rgb]{0.562040,0.190215,0.568721}W} = 0\). This leads to

\[ \large \require{color} \Delta T = \frac{{\color[rgb]{0.334690,0.296180,0.998454}1800}}{10.313 \times {\color[rgb]{0.878548,0.880173,0.060757}0.74}} = {\color[rgb]{0.164799,0.878862,0.723179}235.86\; K} \]

This implies that

\[ \large \require{color} {\color[rgb]{0.164799,0.878862,0.723179}T_2} = {\color[rgb]{0.164799,0.878862,0.723179}235.86} + \left({\color[rgb]{0.164799,0.878862,0.723179}200} + {\color[rgb]{0.164799,0.878862,0.723179}273}\right) = {\color[rgb]{0.164799,0.878862,0.723179}708.86 \; K} \]

Now for an isochoric process we can write

\[ \large \require{color} \frac{{\color[rgb]{0.315209,0.728565,0.037706}p_2}}{{\color[rgb]{0.315209,0.728565,0.037706}p_1}} = \frac{{\color[rgb]{0.164799,0.878862,0.723179}T_2}}{{\color[rgb]{0.164799,0.878862,0.723179}T_1}} \Rightarrow \frac{{\color[rgb]{0.315209,0.728565,0.037706}p_2}}{{\color[rgb]{0.315209,0.728565,0.037706}14}} = \frac{{\color[rgb]{0.164799,0.878862,0.723179}708.86}}{{\color[rgb]{0.164799,0.878862,0.723179}473}} \Rightarrow {\color[rgb]{0.315209,0.728565,0.037706}p_2} = {\color[rgb]{0.315209,0.728565,0.037706}20.98 \; bar}. \]

  1. Here we have:

\[ \large \require{color} {\color[rgb]{0.334690,0.296180,0.998454}Q} = m {\color[rgb]{0.315209,0.728565,0.037706}c}_{\color[rgb]{0.986252,0.007236,0.027423}p} {\color[rgb]{0.164799,0.878862,0.723179}\Delta T} \; \; \; \; \; {\color[rgb]{0.986252,0.007236,0.027423}c}_{\color[rgb]{0.315209,0.728565,0.037706}p} = R + {\color[rgb]{0.878548,0.880173,0.060757}c}_{\color[rgb]{0.079785,0.618358,0.483717}V} \]

\[ \large \require{color} {\color[rgb]{0.986252,0.007236,0.027423}c}_{\color[rgb]{0.315209,0.728565,0.037706}p} = 0.287 + {\color[rgb]{0.878548,0.880173,0.060757}0.74} = {\color[rgb]{0.986252,0.007236,0.027423}1.027 \; \frac{kJ}{kg \cdot K}} \]

From this we can compute

\[ \large \require{color} {\color[rgb]{0.164799,0.878862,0.723179}\Delta T} = \frac{{\color[rgb]{0.334690,0.296180,0.998454}1800}}{10.313 \times {\color[rgb]{0.986252,0.007236,0.027423}1.027}} \Rightarrow {\color[rgb]{0.164799,0.878862,0.723179}\Delta T} = {\color[rgb]{0.164799,0.878862,0.723179}169.95} \]

This leads to

\[ \large \require{color} {\color[rgb]{0.164799,0.878862,0.723179}T_2} = {\color[rgb]{0.164799,0.878862,0.723179}642.95 \; K} \]

To work out the volume for an isobaric process we make use of the equation of state

\[ \large \require{color} \frac{{\color[rgb]{0.079785,0.618358,0.483717}V_2}}{{\color[rgb]{0.079785,0.618358,0.483717}V_1}} = \frac{{\color[rgb]{0.164799,0.878862,0.723179}T_2}}{{\color[rgb]{0.164799,0.878862,0.723179}T_1}} \Rightarrow {\color[rgb]{0.079785,0.618358,0.483717}V_2} = \frac{{\color[rgb]{0.079785,0.618358,0.483717}1} \times {\color[rgb]{0.164799,0.878862,0.723179}642.95}}{{\color[rgb]{0.164799,0.878862,0.723179}473}} = {\color[rgb]{0.079785,0.618358,0.483717}1.36} \;{\color[rgb]{0.079785,0.618358,0.483717} m^3} \]

  1. From the Clausius inequality,

\[ \large \require{color} {\color[rgb]{0.599997,0.600015,0.600005}dS} = \frac{{\color[rgb]{0.334690,0.296180,0.998454}dQ_{rev}}}{{\color[rgb]{0.164799,0.878862,0.723179}T}} + {\color[rgb]{0.599997,0.600015,0.600005}dS_{irrev}} \]

it is clear that since heat is being added, $ > 0 $ entropy cannot remain constant.

Problem 6

On a T-s diagram, draw, clearly label, and justify the trends for the following involving a perfect gas

  1. constant enthalpy

  2. constant pressure

  3. constant density

  4. reversible and adiabatic.

Solution

Please see the diagram below.

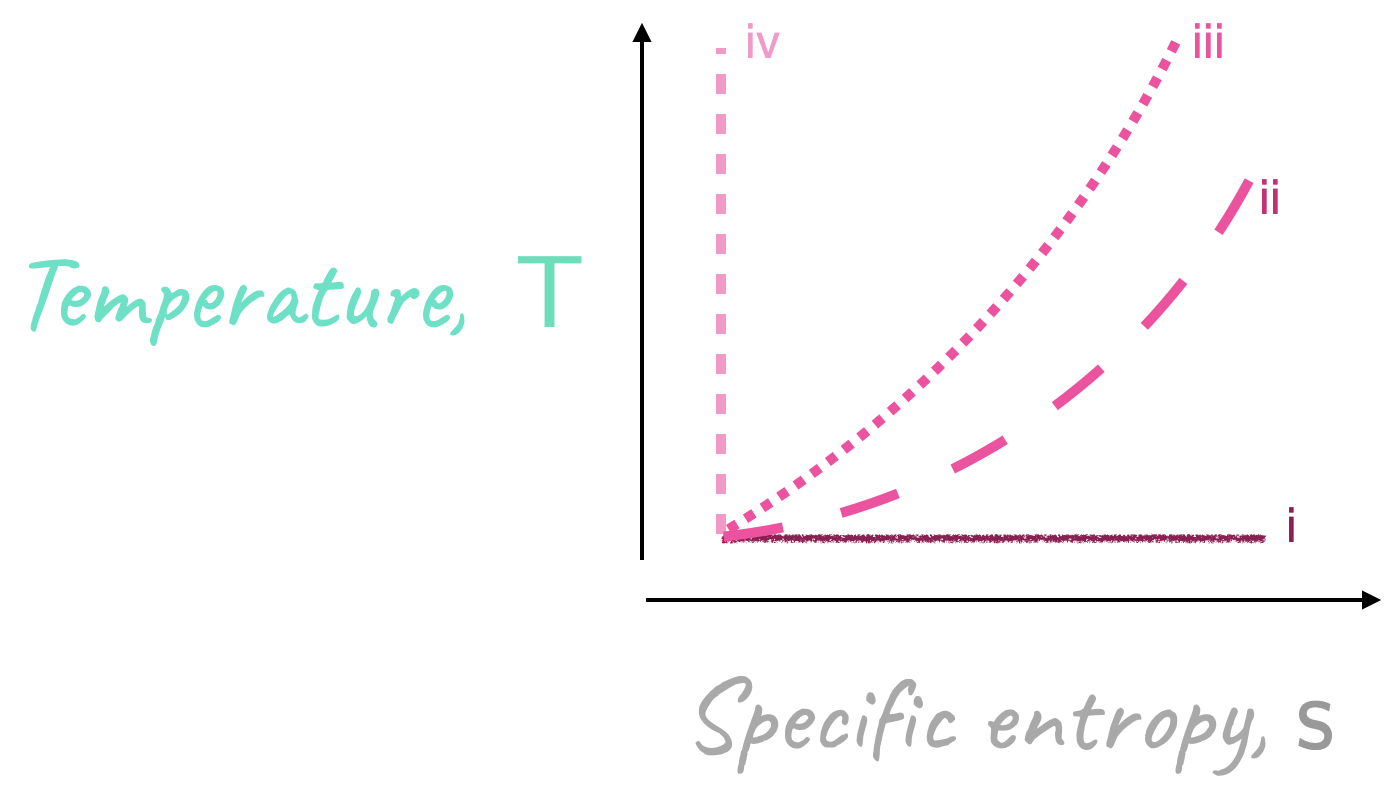
cycle

  1. For a perfect gas, \(\require{color}{\color[rgb]{0.986252,0.007236,0.027423}h} = {\color[rgb]{0.986252,0.007236,0.027423}c}_{\color[rgb]{0.315209,0.728565,0.037706}p} {\color[rgb]{0.164799,0.878862,0.723179}T} + constant\). Hence, a constant \(\require{color}{\color[rgb]{0.986252,0.007236,0.027423}h}\) line is a constant \(\require{color}{\color[rgb]{0.164799,0.878862,0.723179}T}\) line.

  2. We know that for a constant pressure process

\[ \large \require{color} {\color[rgb]{0.164799,0.878862,0.723179}T}{\color[rgb]{0.599997,0.600015,0.600005}ds} = {\color[rgb]{0.986252,0.007236,0.027423}dh} - {\color[rgb]{0.918231,0.469102,0.038229}\nu} {\color[rgb]{0.315209,0.728565,0.037706}dp} = {\color[rgb]{0.986252,0.007236,0.027423}dh} \]

So for a perfect gas

\[ \large \require{color} {\color[rgb]{0.986252,0.007236,0.027423}dh} = {\color[rgb]{0.986252,0.007236,0.027423}c}_{\color[rgb]{0.315209,0.728565,0.037706}p} {\color[rgb]{0.164799,0.878862,0.723179}dT} \Rightarrow \frac{{\color[rgb]{0.164799,0.878862,0.723179}dT}}{{\color[rgb]{0.599997,0.600015,0.600005}ds}} = \frac{{\color[rgb]{0.164799,0.878862,0.723179}T}}{{\color[rgb]{0.986252,0.007236,0.027423}c}_{\color[rgb]{0.315209,0.728565,0.037706}p}} \]

we anticipate a curve with a positive slope with the gradient increasing with temperature.

  1. For a constant volume process, using the same process as above we can derive (see Lecture 17 for more background)

\[ \large \require{color} \mathsf{\frac{{\color[rgb]{0.164799,0.878862,0.723179}dT}}{{\color[rgb]{0.599997,0.600015,0.600005}ds}} = \frac{{\color[rgb]{0.164799,0.878862,0.723179}T}}{{\color[rgb]{0.878548,0.880173,0.060757}c}_{\color[rgb]{0.079785,0.618358,0.483717}V}} } \]

where \({\color[rgb]{0.986252,0.007236,0.027423}c}_{\color[rgb]{0.315209,0.728565,0.037706}p} > {\color[rgb]{0.878548,0.880173,0.060757}c}_{\color[rgb]{0.079785,0.618358,0.483717}V}\), and thus the trend for this is the same as in ii but with an increased gradient.

  1. This is equivalent to an isentropic process, which is a vertical line.