L22 examples
Problem 1
Consider the engine of the supersonic aircraft, the concorde. A schematic of the engine is given below. For an intake in such an aircraft, the flow must be decelerated to subsonic speeds before it enters the compressor.

(image above from Unsplash by Lynn Kintziger)
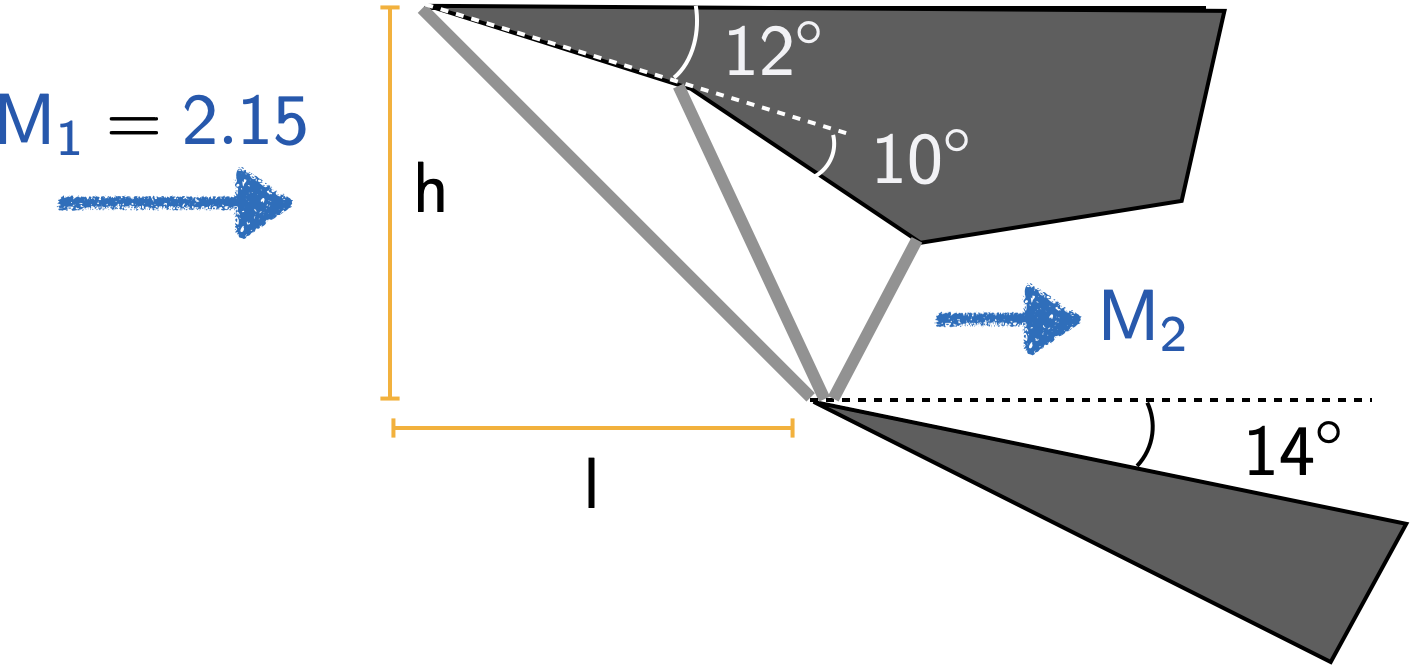
Calculate \(M_2\).
Express the distance \(l\) as a function of \(h\).
Find the fractional loss in stagnation pressure.
Assume \(\gamma=1.4\).
Solution
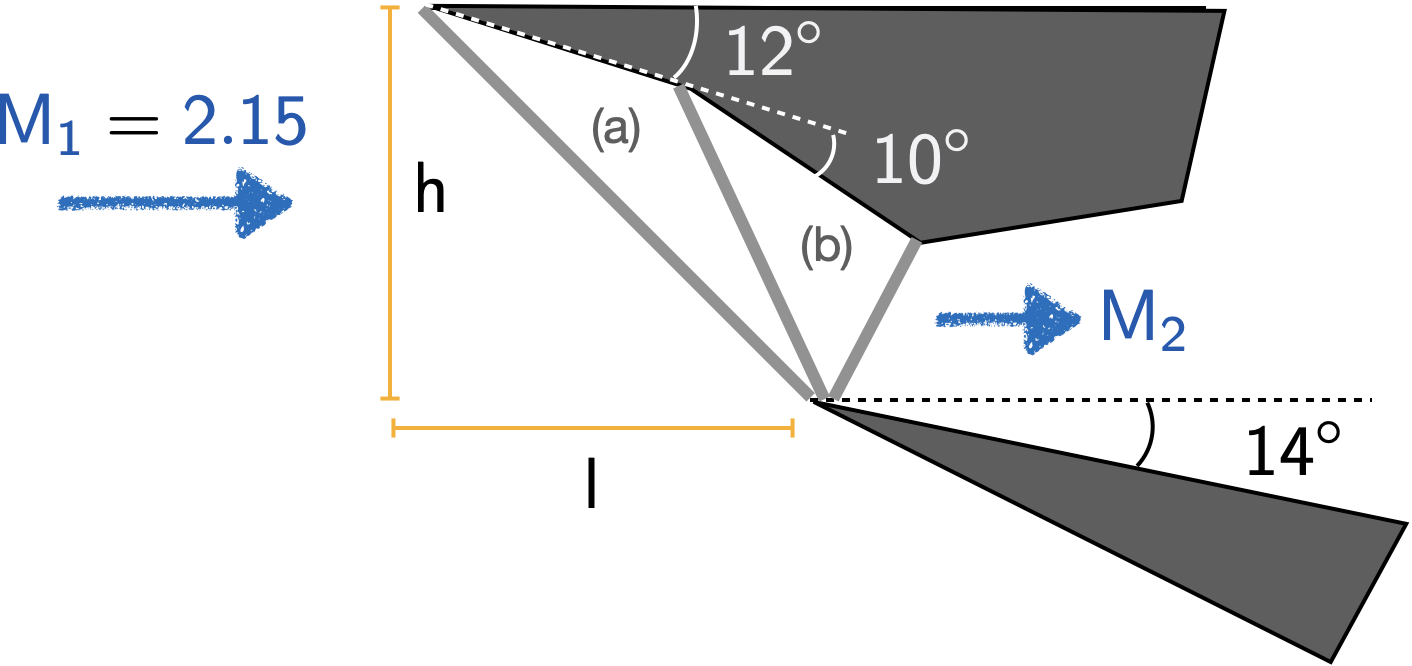
- First, we amend the diagram with regions \((a)\) and \((b)\) as shown below.
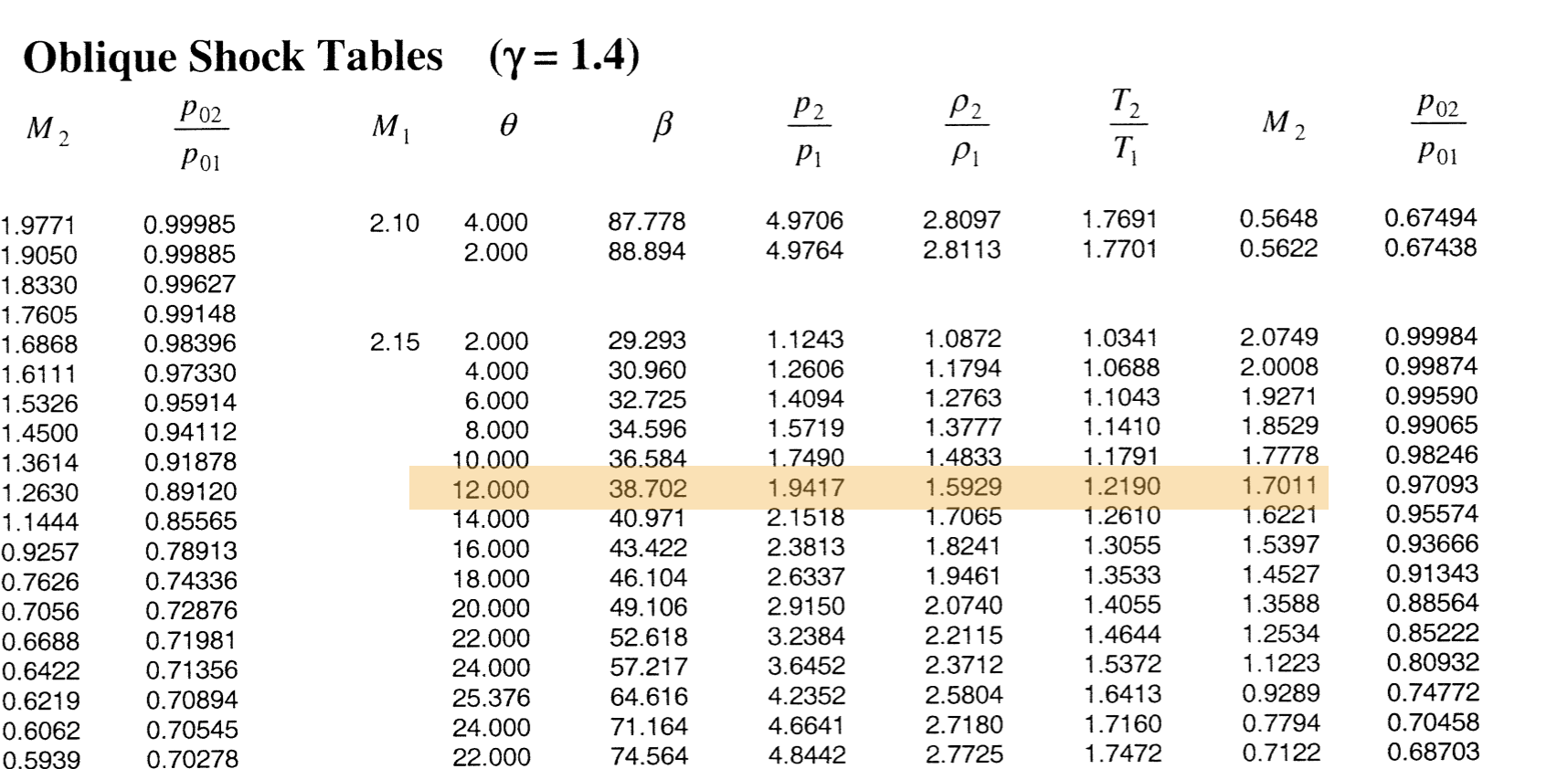
Consider the oblique shock tables with an inlet Mach number of \(\require{color}{\color[rgb]{0.041732,0.352132,0.699576}M_1} = {\color[rgb]{0.041732,0.352132,0.699576}2.15}, \; \; \theta = 12^{\circ}\). As shown below, this leads to an exit Mach number of \(\require{color}{\color[rgb]{0.041732,0.352132,0.699576}M_a} = {\color[rgb]{0.041732,0.352132,0.699576}1.7011}\) and a wave angle of \(\require{color}{\color[rgb]{0.131302,0.999697,0.023594}\beta} = {\color[rgb]{0.131302,0.999697,0.023594}38.72^{\circ}}\). This is just for the first shock.
For the second shock we are given the wedge angle to be \(\theta = 10^{\circ}\) and \(\require{color}{\color[rgb]{0.041732,0.352132,0.699576}M_2} = {\color[rgb]{0.041732,0.352132,0.699576}1.7011}\). Once again consulting the tables (see below) we arrive at \(\require{color}{\color[rgb]{0.041732,0.352132,0.699576}M_b} = {\color[rgb]{0.041732,0.352132,0.699576}1.347}\). Note that this corresponds to the supersonic solution and not the subsonic one.
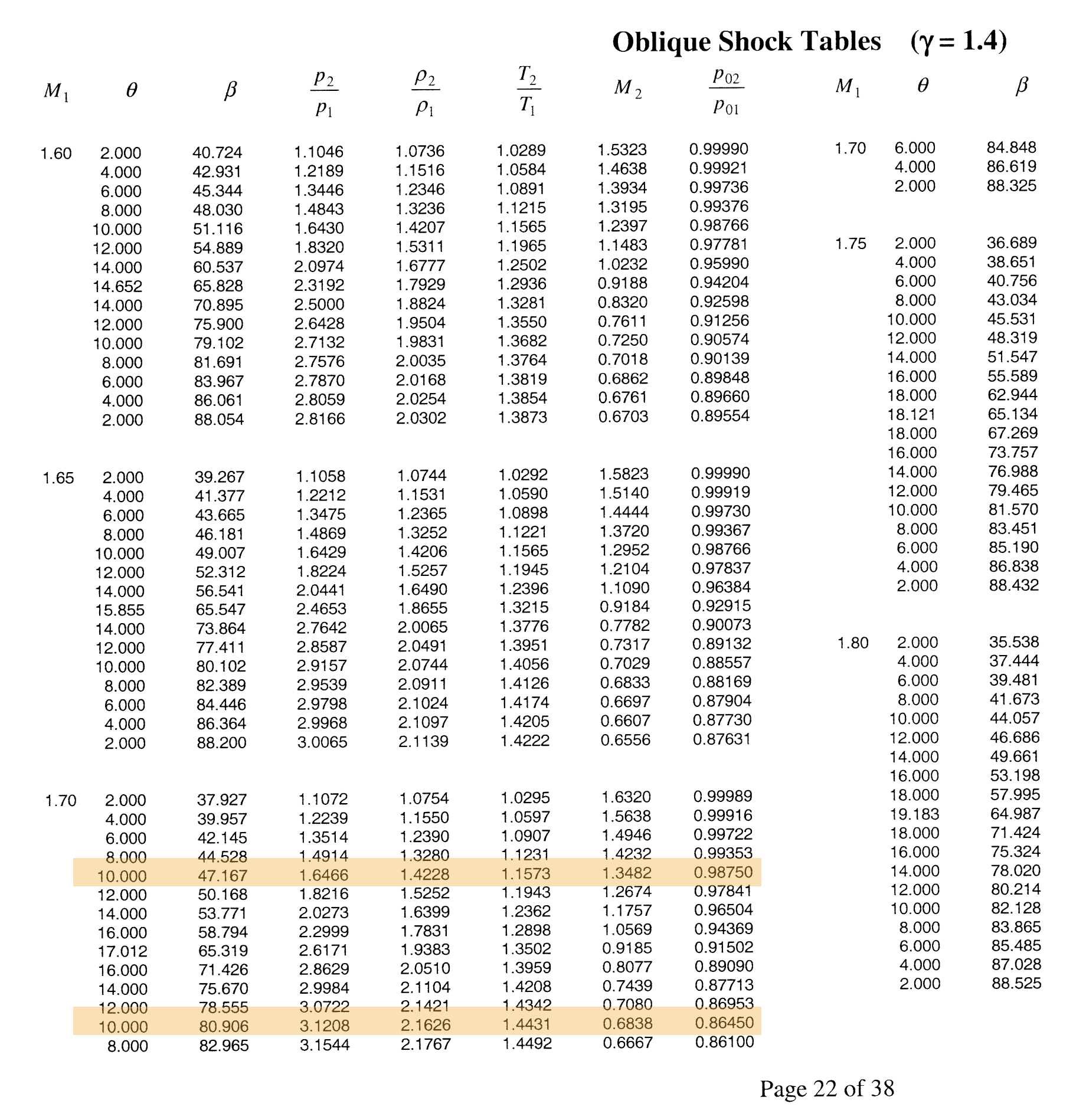
The third and final shock has a wedge angle given by \(\theta = 22^{\circ} - 14^{\circ} = 8^{\circ}\). At this wedge angle, we once again take the first (or the weaker) solution, which yields \(\require{color}{\color[rgb]{0.041732,0.352132,0.699576}M_2} = {\color[rgb]{0.041732,0.352132,0.699576}0.95}\).
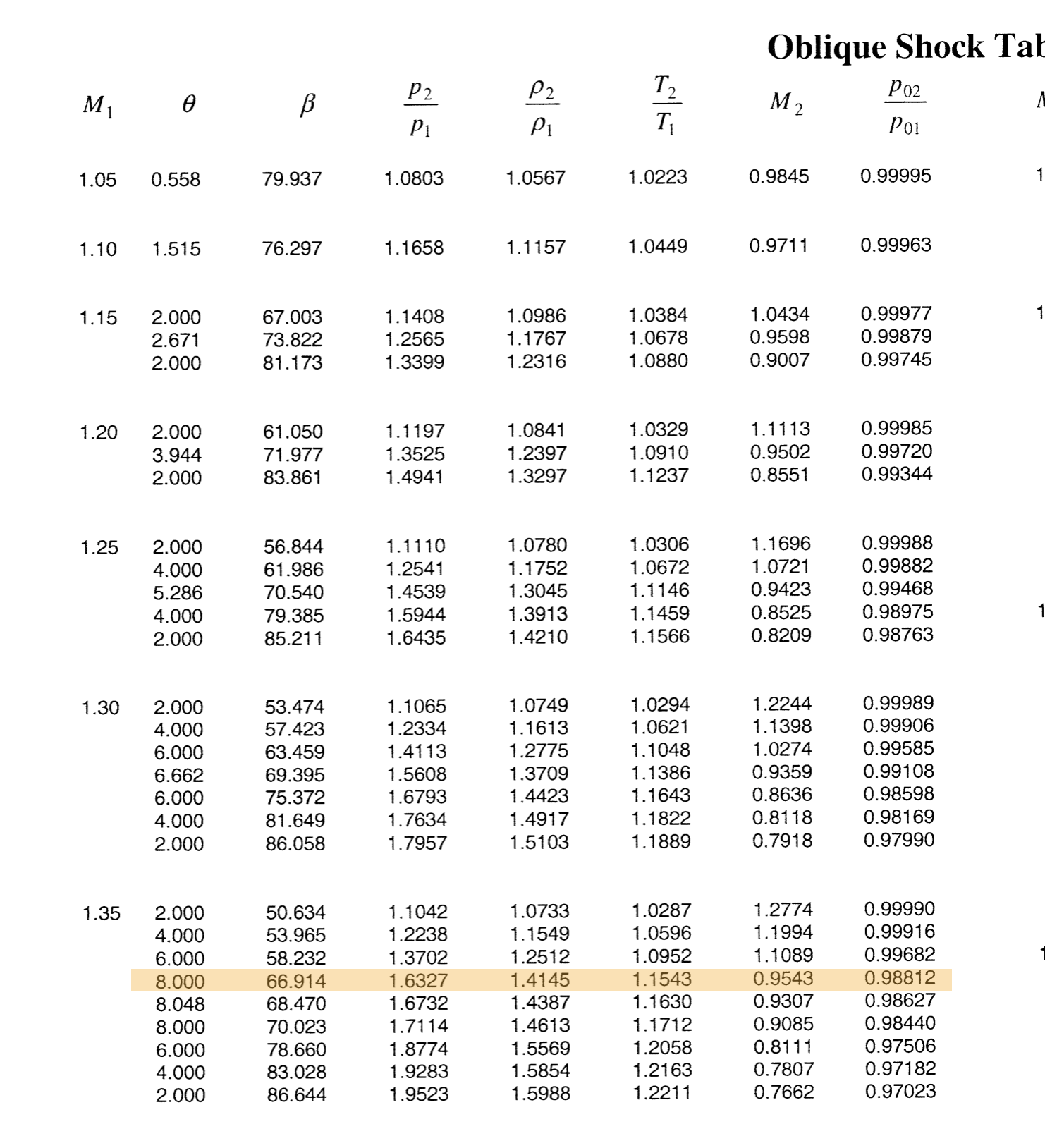
- Next, to work out the relationship between \(h\) and \(l\) we note that
\[ \large \require{color} tan \left( {\color[rgb]{0.131302,0.999697,0.023594}\beta} \right) = \frac{h}{l} \Rightarrow tan \left({\color[rgb]{0.131302,0.999697,0.023594}38.702^{\circ}}\right) = \frac{h}{l} \Rightarrow l = 1.25 h \]
- To work out the pressure losses, we make use of the stagnation pressure ratios:
\[ \large \require{color} \frac{{\color[rgb]{0.315209,0.728565,0.037706}p_{02}}}{{\color[rgb]{0.315209,0.728565,0.037706}p_{01}}} = \frac{{\color[rgb]{0.315209,0.728565,0.037706}p_{02}}}{{\color[rgb]{0.315209,0.728565,0.037706}p_{0b}}} \frac{{\color[rgb]{0.315209,0.728565,0.037706}p_{0b}}}{{\color[rgb]{0.315209,0.728565,0.037706}p_{0a}}} \frac{{\color[rgb]{0.315209,0.728565,0.037706}p_{0a}}}{{\color[rgb]{0.315209,0.728565,0.037706}p_{01}}} = 0.97093 \times 0.9875 \times 0.98812 = 0.9473 \]
Problem 2
The figure below shows a Prandtl-Meyer expansion fan, with an upstream Mach number of \(\mathsf{1.86}\) and a flow deflection angle of \(\mathsf{20^{\circ}}\). You may find the table useful, along with its corresponding identity
\[ \large \require{color} {\color[rgb]{0.986252,0.007236,0.027423}\nu} \left( {\color[rgb]{0.041732,0.352132,0.699576}M} \right) = \sqrt{\frac{\gamma + 1}{\gamma - 1}} tan^{-1}\left(\sqrt{\frac{\gamma - 1}{\gamma + 1} \left( {\color[rgb]{0.041732,0.352132,0.699576}M}^2 - 1\right) } \right) - tan^{-1}\left( \sqrt{{\color[rgb]{0.041732,0.352132,0.699576}M}^2 - 1} \right). \]
| Mach number | \(\nu\) (all in degrees) |
|---|---|
| 2.25 | 33.018 |
| 2.35 | 35.525 |
| 2.45 | 37.945 |
| 2.55 | 40.279 |
| 2.65 | 42.529 |
| 2.75 | 44.694 |
| 2.85 | 46.778 |
Calculate the downstream Mach number, \({\color[rgb]{0.041732,0.352132,0.699576}M_2}\)
How does the static density, static pressure and static enthalpy vary across the expansion fan?
Is the stagnation pressure constant across an expansion fan?
Solution
- Plugging in a value of \(\require{color}{\color[rgb]{0.041732,0.352132,0.699576}M_1} = {\color[rgb]{0.041732,0.352132,0.699576}1.86}\) in the formula above, yields \(\require{color}{\color[rgb]{0.986252,0.007236,0.027423}\nu_1} = {\color[rgb]{0.986252,0.007236,0.027423}0.3918}\). Note that this value is in radians; to convert it to degrees, we have
\[ \large \require{color} {\color[rgb]{0.986252,0.007236,0.027423}\nu_1} = {\color[rgb]{0.986252,0.007236,0.027423}0.3918} \; \; \Rightarrow \; \; {\color[rgb]{0.986252,0.007236,0.027423}\nu_1}= {\color[rgb]{0.986252,0.007236,0.027423}0.3918} \times \frac{180}{\pi} = 22.44^{\circ} \]
Now, from the problem description, we know that \(\mathsf{\theta = 20^{\circ}}\). Thus,
\[ \large \require{color} \theta = {\color[rgb]{0.986252,0.007236,0.027423}\nu_2} - {\color[rgb]{0.986252,0.007236,0.027423}\nu_1} \; \; \Rightarrow \; \; {\color[rgb]{0.986252,0.007236,0.027423}\nu_2} = \theta + {\color[rgb]{0.986252,0.007236,0.027423}\nu_1} = 42.44^{\circ} \]
From the table above, we know that \(\require{color}{\color[rgb]{0.041732,0.352132,0.699576}M_2} \approx {\color[rgb]{0.041732,0.352132,0.699576}2.65}\).
The static density decreases, the static pressure decreases, and the static enthalpy also decreases
Yes, the stagnation pressure stays constant.