A quantity of dry air is slowly compressed in a cylinder by means of a piston, until its volume is halved. The initial pressure and volume are \(\require{color}{\color[rgb]{0.315209,0.728565,0.037706}1 \; bar \; \; (10^5\; Pa)}\) and \(\require{color}{\color[rgb]{0.079785,0.618358,0.483717}1 \;liter}\) respectively, and during the compression the pressure varies inversely with the volume. Sketch the process on a \(\require{color}{\color[rgb]{0.315209,0.728565,0.037706}p}-{\color[rgb]{0.079785,0.618358,0.483717}V}\) diagram and calculate the work transfer. Is this a positive or negative quantity?
Note that 1 liter is \(10^{-3} \; m^3\). Consider the diagram below; the work done is given by
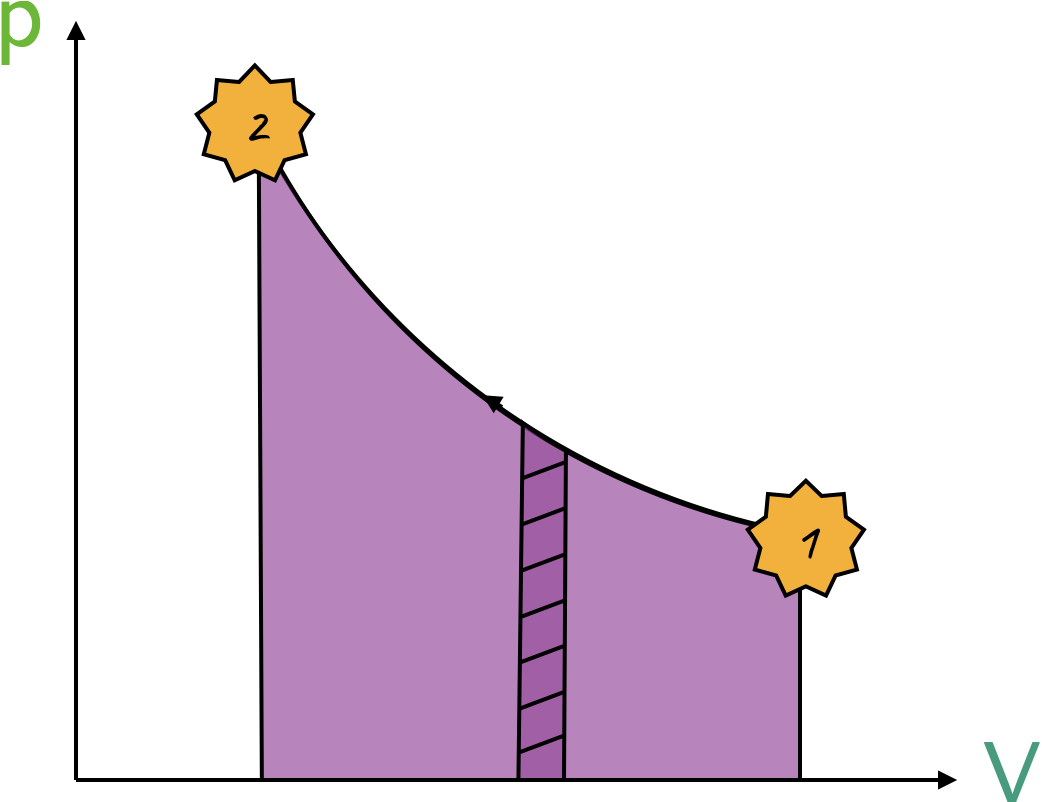
\[ \large \require{color} {\color[rgb]{0.562040,0.190215,0.568721}W} = \int_{{\color[rgb]{0.079785,0.618358,0.483717}V}_1}^{{\color[rgb]{0.079785,0.618358,0.483717}V}_2} {\color[rgb]{0.315209,0.728565,0.037706}p}d{\color[rgb]{0.079785,0.618358,0.483717}V} = \int_{{\color[rgb]{0.079785,0.618358,0.483717}V}_1}^{{\color[rgb]{0.079785,0.618358,0.483717}V}_2} \frac{C}{{\color[rgb]{0.079785,0.618358,0.483717}V}} d{\color[rgb]{0.079785,0.618358,0.483717}V} = \left[ C \; ln \left( {\color[rgb]{0.079785,0.618358,0.483717}V} \right) \right]_{{\color[rgb]{0.079785,0.618358,0.483717}V}_1}^{{\color[rgb]{0.079785,0.618358,0.483717}V}_2}. \]
From the conditions at state 1, we have
\[ \large \require{color} C = {\color[rgb]{0.315209,0.728565,0.037706}p}_1 {\color[rgb]{0.079785,0.618358,0.483717}V}_1 = {\color[rgb]{0.315209,0.728565,0.037706}p}_2 {\color[rgb]{0.079785,0.618358,0.483717}V}_2, \]
yielding
\[ \large \require{color} {\color[rgb]{0.562040,0.190215,0.568721}W} = {\color[rgb]{0.315209,0.728565,0.037706}p}_1 {\color[rgb]{0.079785,0.618358,0.483717}V}_1 ln \left( \frac{{\color[rgb]{0.079785,0.618358,0.483717}V}_2}{{\color[rgb]{0.079785,0.618358,0.483717}V}_1} \right) = {\color[rgb]{0.315209,0.728565,0.037706}10^{5} }\times {\color[rgb]{0.079785,0.618358,0.483717}10^{-3}} \times ln \left( \frac{{\color[rgb]{0.079785,0.618358,0.483717}1}}{{\color[rgb]{0.079785,0.618358,0.483717}2}} \right) \]
Solving the aboveimport numpy as np
work = 10**5 * 10**(-3) * np.log(0.5)
print(str(work)+' J')
print('The work is negative and thus the work is transferred to the system.')-69.31471805599453 J
The work is negative and thus the work is transferred to the system.