L20 examples

Problem 1

A pitot tube mounted on an aircraft flying at an altitude of \(10,000\) meters measures a pressure of \(\require{color}{\color[rgb]{0.315209,0.728565,0.037706}16\; kPa}\) relative to static. Determine the flight speed.

(image above by David Monniaux)

Solution

In this problem, we will make use of look-up tables; these will typically be given to you for a problem. Consider the three snippets given below.

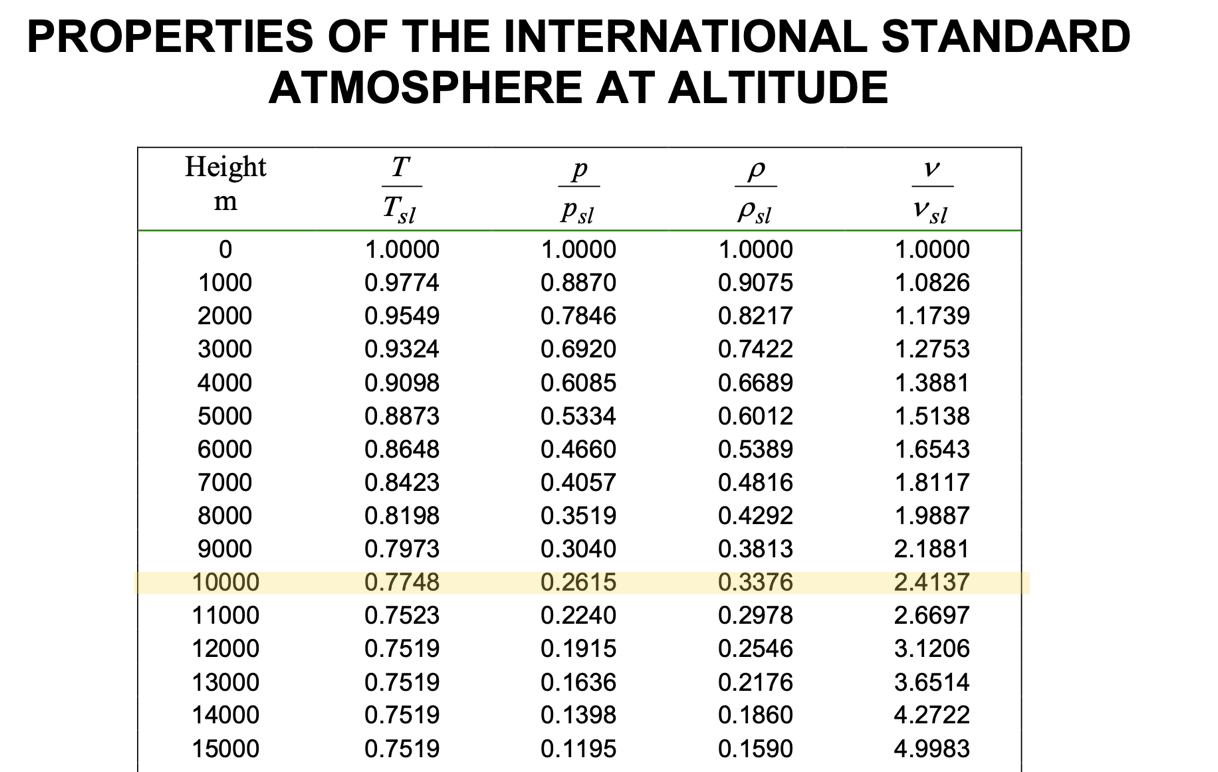
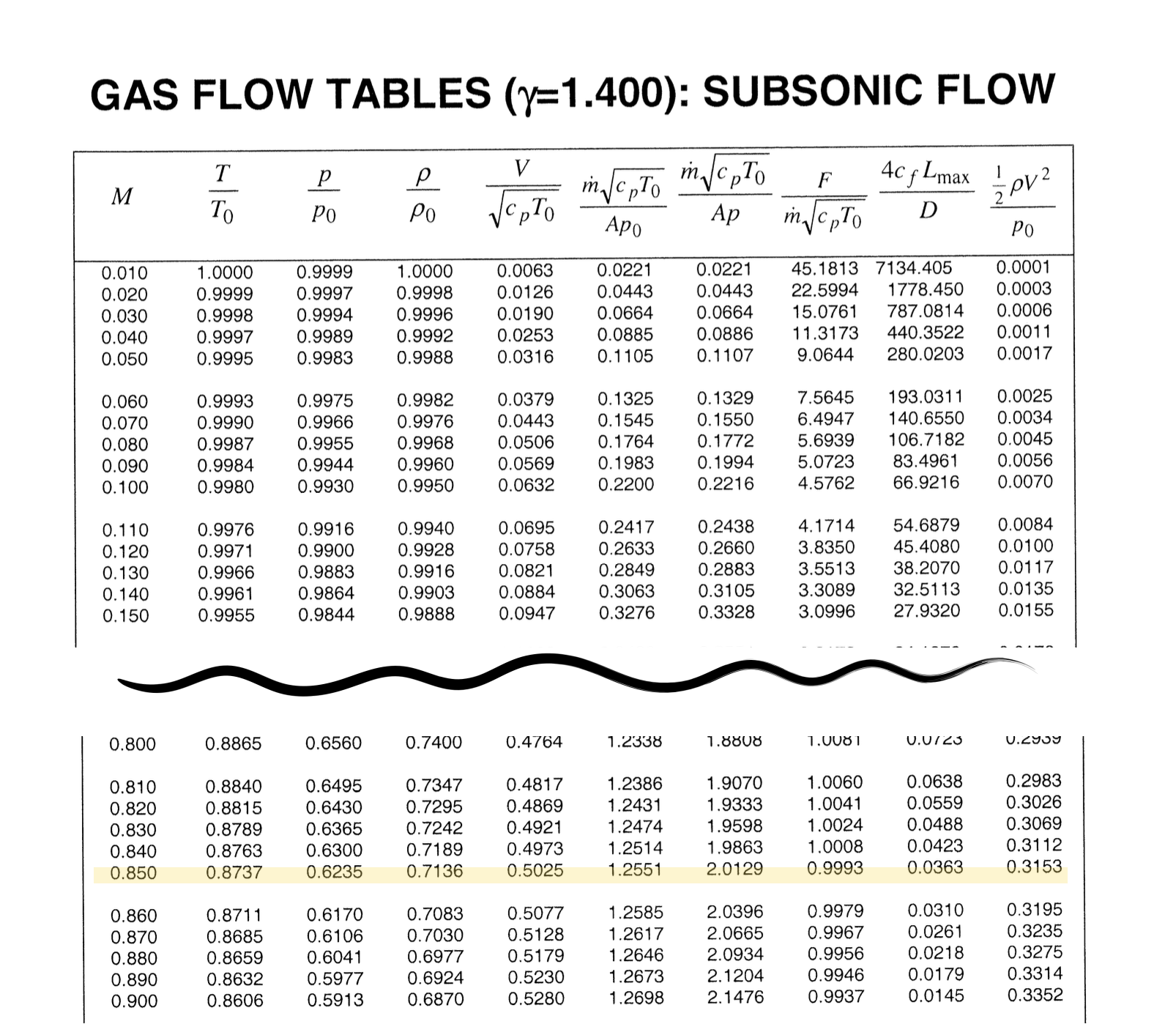
We can work out the static temperatures and pressures at this altitude, i.e.,

\[ \large \require{color} {\color[rgb]{0.164799,0.878862,0.723179}T} = 0.7788 \times \left( {\color[rgb]{0.164799,0.878862,0.723179}15^{\circ}} + {\color[rgb]{0.164799,0.878862,0.723179}273.15 K} \right) = {\color[rgb]{0.164799,0.878862,0.723179}223.3 \; K} \]

\[ \large \require{color} {\color[rgb]{0.315209,0.728565,0.037706}p} = {\color[rgb]{0.315209,0.728565,0.037706}0.2615} \times {\color[rgb]{0.315209,0.728565,0.037706}101325} \; {\color[rgb]{0.315209,0.728565,0.037706}Pa} = {\color[rgb]{0.315209,0.728565,0.037706}26.5 \; kPa} \]

The pitot tube measures

\[ \large \require{color} {\color[rgb]{0.315209,0.728565,0.037706}\Delta p} = {\color[rgb]{0.315209,0.728565,0.037706}p_0} - {\color[rgb]{0.315209,0.728565,0.037706}p} = {\color[rgb]{0.315209,0.728565,0.037706}16 \; kPa} \]

This, the stagnation pressure is given by:

\[ \large \require{color} {\color[rgb]{0.315209,0.728565,0.037706}p_0} = {\color[rgb]{0.315209,0.728565,0.037706}16} + {\color[rgb]{0.315209,0.728565,0.037706}26.5} = {\color[rgb]{0.315209,0.728565,0.037706}42.5 \; kPa} \]

and the pressure ratio is therefore

\[ \large \require{color} {\color[rgb]{0.315209,0.728565,0.037706}\frac{p}{p_0}} = \frac{{\color[rgb]{0.315209,0.728565,0.037706}26.5}}{{\color[rgb]{0.315209,0.728565,0.037706}42.5}} = {\color[rgb]{0.315209,0.728565,0.037706}0.6235} \]

From the subsonic flow look-up tables, the Mach number for this pressure ratio is given to be \(\require{color}{\color[rgb]{0.041732,0.352132,0.699576}M} = {\color[rgb]{0.041732,0.352132,0.699576}0.85}\). However, we need to convert this to a velocity value in meters per second. Note that the speed of sound at \(10,000\) meters is given by

\[ \large \require{color} {\color[rgb]{0.985542,0.009453,0.999181}a}^2 = \gamma R {\color[rgb]{0.164799,0.878862,0.723179}T} = 1.4 \times 287 \times {\color[rgb]{0.164799,0.878862,0.723179}223.3 \; K} = {\color[rgb]{0.985542,0.009453,0.999181}299.5 \; m/s} \]

Thus, the flight speed is

\[ \large \require{color} {\color[rgb]{0.059472,0.501943,0.998465}v} = {\color[rgb]{0.041732,0.352132,0.699576}M}{\color[rgb]{0.985542,0.009453,0.999181}a} = {\color[rgb]{0.041732,0.352132,0.699576}0.85} \times {\color[rgb]{0.985542,0.009453,0.999181}299.5 \; m/s} = {\color[rgb]{0.000066,0.001801,0.998229}254.4 \; m/s} \]