Problem 1

A reservoir contains a volume of water 1 meter in height. Someone has accidentally spilled a tiny bit of oil, which floats on top of the water. The oil has a height of 0.2 meters. Please calculate the gauge pressure at the bottom of the reservoir. Assume the following densities for oil and water \(\require{color}{\color[rgb]{0.964810,0.470942,0.057578}\rho_{o}} = \require{color}{\color[rgb]{0.964810,0.470942,0.057578}750 kg / m^3}\) and \(\require{color}{\color[rgb]{0.964810,0.470942,0.057578}\rho_{w}} = \require{color}{\color[rgb]{0.964810,0.470942,0.057578}1000 kg / m^3}\).

reservoir

Solution

It will be useful to consider a diagram of the reservoir.

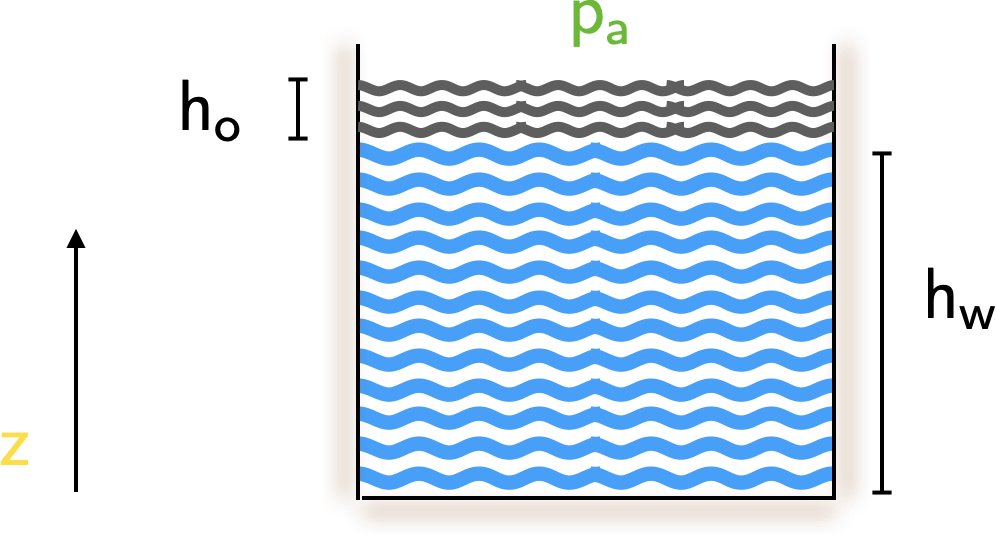
reservoir

At the interface \(i\), the pressure is given by

\[ \large \require{color}{\color[rgb]{0.315209,0.728565,0.037706}p_i }= {\color[rgb]{0.315209,0.728565,0.037706}p_a} + {\color[rgb]{0.964810,0.470942,0.057578}\rho_{o}} g h_o. \]

At the reservoir floor, the pressure is given by

\[ \large \require{color}{\color[rgb]{0.315209,0.728565,0.037706}p }= {\color[rgb]{0.315209,0.728565,0.037706}p_i} + {\color[rgb]{0.964810,0.470942,0.057578}\rho{w}} g h_w. \]

This results in

\[ \large \require{color}{\color[rgb]{0.315209,0.728565,0.037706}p }= {\color[rgb]{0.315209,0.728565,0.037706}p_a} + {\color[rgb]{0.964810,0.470942,0.057578}\rho_{o}} g h_o + {\color[rgb]{0.964810,0.470942,0.057578}\rho_{w}} g h_w. \]

Now, the definition of the gauge pressure is the pressure measurement relative to the atmospheric pressure. That is

\[ \large \require{color}{\color[rgb]{0.315209,0.728565,0.037706}p } - {\color[rgb]{0.315209,0.728565,0.037706}p_a}= {\color[rgb]{0.964810,0.470942,0.057578}\rho_{o}} g h_o + {\color[rgb]{0.964810,0.470942,0.057578}\rho_{w}} g h_w. \]

Plugging in values for the above, we arrive at

\[ \large \require{color}{\color[rgb]{0.315209,0.728565,0.037706}p } - {\color[rgb]{0.315209,0.728565,0.037706}p_a}= {\color[rgb]{0.964810,0.470942,0.057578} 750 \frac{kg}{m^3}} \times 9.8 \frac{m}{s^2} \times 0.2 m + {\color[rgb]{0.964810,0.470942,0.057578} 1000 \frac{kg}{m^3}} \times 9.8 \frac{m}{s^2} \times 1 m. \]

\[ \large \require{color}{\color[rgb]{0.315209,0.728565,0.037706}p } - {\color[rgb]{0.315209,0.728565,0.037706}p_a} = 11,270 \frac{kg }{m \cdot s^2} \] This may also be expressed as \(11,270 \; Pa\), where \(Pa\) stands for Pascals.

Problem 2

An orifice plate is a thin circular plate with an orifice (hole) that is machined through its center. Below you will find a few pictures of an orifice plate and how it is used to control the flow. Essentially, one can use an orifice plate within a pipe to induce a pressure drop. This pressure drop is used to work out the velocity of the flow going through the pipe.

Side view of plate in a pipe Orifice plate measurement system
orifice orifice

Now consider a sloping manometer that is used to measure the pressure drop across an orifice plate, in a horizontal pipe carrying a fluid (air). The manometer is slanted, with \(\require{color}{\color[rgb]{0.127700,0.999775,0.999047}\gamma } = 30^{\circ}\). The arrangement is shown below.

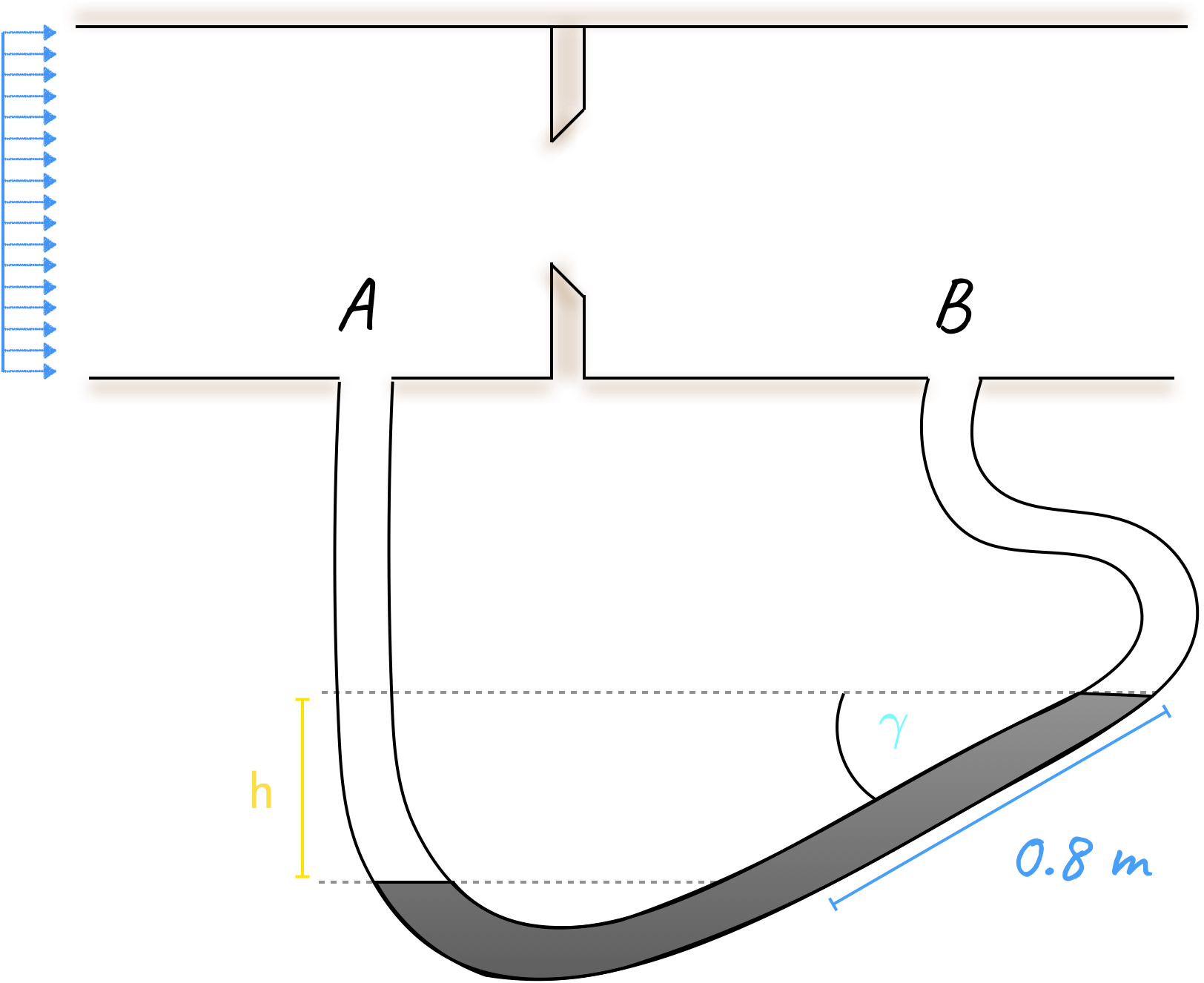
orifice

If the liquid in the manometer is mercury, which has a density of \(\require{color}{\color[rgb]{0.964810,0.470942,0.057578}\rho_{m}} = \require{color}{\color[rgb]{0.964810,0.470942,0.057578}13.6 \times 10^3 \; kg/m^3}\), find the pressure drop.

Solution

We will ignore the contribution of the weight of air. This is because the density of mercury is roughly four orders of magnitude greater. Thus, the pressure drop may be expressed as

\[ \large \require{color}{\color[rgb]{0.315209,0.728565,0.037706}p_{A} }- {\color[rgb]{0.315209,0.728565,0.037706}p_{B} }= {\color[rgb]{0.918231,0.469102,0.038229}\rho_{m}} g {\color[rgb]{1.000000,0.869732,0.000000}h} \]

\[ \large \require{color}{\color[rgb]{0.315209,0.728565,0.037706}p_{A} }- {\color[rgb]{0.315209,0.728565,0.037706}p_{B} }= {\color[rgb]{0.918231,0.469102,0.038229}13.6 \times 10^{3} \frac{kg}{m^3}} \times 9.8 \frac{m}{s^2} \times {\color[rgb]{0.000000,0.869732,0.900000}0.8 m} \times sin \left({\color[rgb]{0.127700,0.999775,0.999047} 30^{\circ}}\right) \]

\[ \large \require{color}{\color[rgb]{0.315209,0.728565,0.037706}p_{A} }- {\color[rgb]{0.315209,0.728565,0.037706}p_{B} }= 53,312 \frac{N}{m^2} \]

Problem 3

A mercury barometer column with a density of \(\require{color}{\color[rgb]{0.964810,0.470942,0.057578}\rho_{l}} = \require{color}{\color[rgb]{0.964810,0.470942,0.057578}13,600 kg / m^3}\) has a height of \(\require{color}{\color[rgb]{0.986048,0.008333,0.501924}h} = {\color[rgb]{0.986048,0.008333,0.501924}0.75 m}\). What is the local atmospheric pressure?

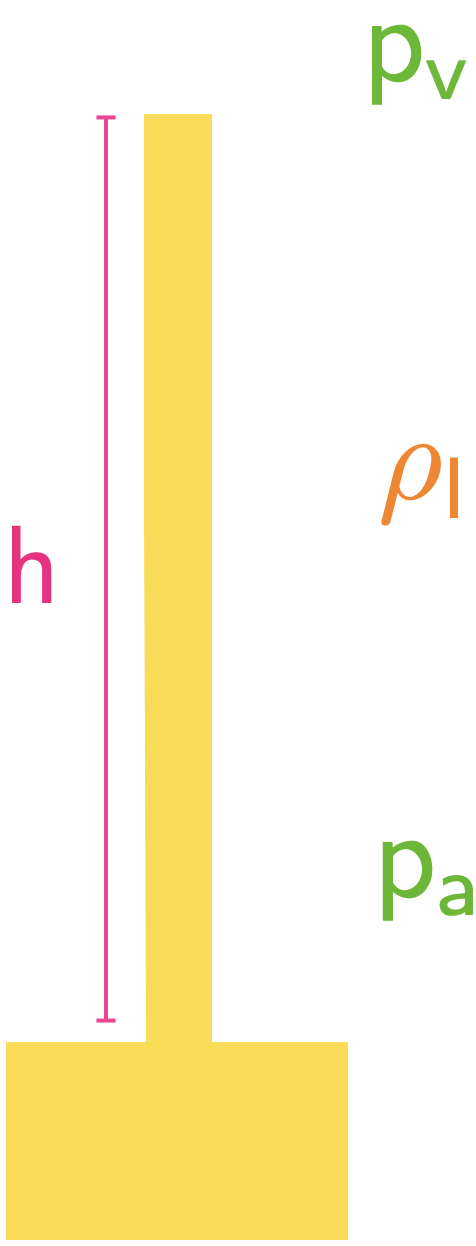
orifice

Solution

The difference in pressures may be expressed as:

\[ \large \require{color}{\color[rgb]{0.315209,0.728565,0.037706}p_a} - {\color[rgb]{0.315209,0.728565,0.037706}p_{v}} = \left( {\color[rgb]{0.918231,0.469102,0.038229}\rho_{l}} - {\color[rgb]{0.918231,0.469102,0.038229}\rho_{a}} \right) g {\color[rgb]{0.985542,0.009453,0.999181}h} \approx \rho_{l} g {\color[rgb]{0.985542,0.009453,0.999181}h} \]

Additionally, since \({\color[rgb]{0.315209,0.728565,0.037706}p_{v}} \approx 0\), we have

\[ \large \require{color}{\color[rgb]{0.315209,0.728565,0.037706}p_a} \approx \rho_{l} g {\color[rgb]{0.985542,0.009453,0.999181}h} \]

Numerical solution is given below.
Code 
h = 0.75
rho = 13600
g = 9.8
p_a = rho * h * g
print(str(p_a/101325)+' atm')
0.9865284974093265 atm

Problem 4

Consider a dam which has a parabolic surface as shown in the figure below.

Real perspective Schematic for the problem
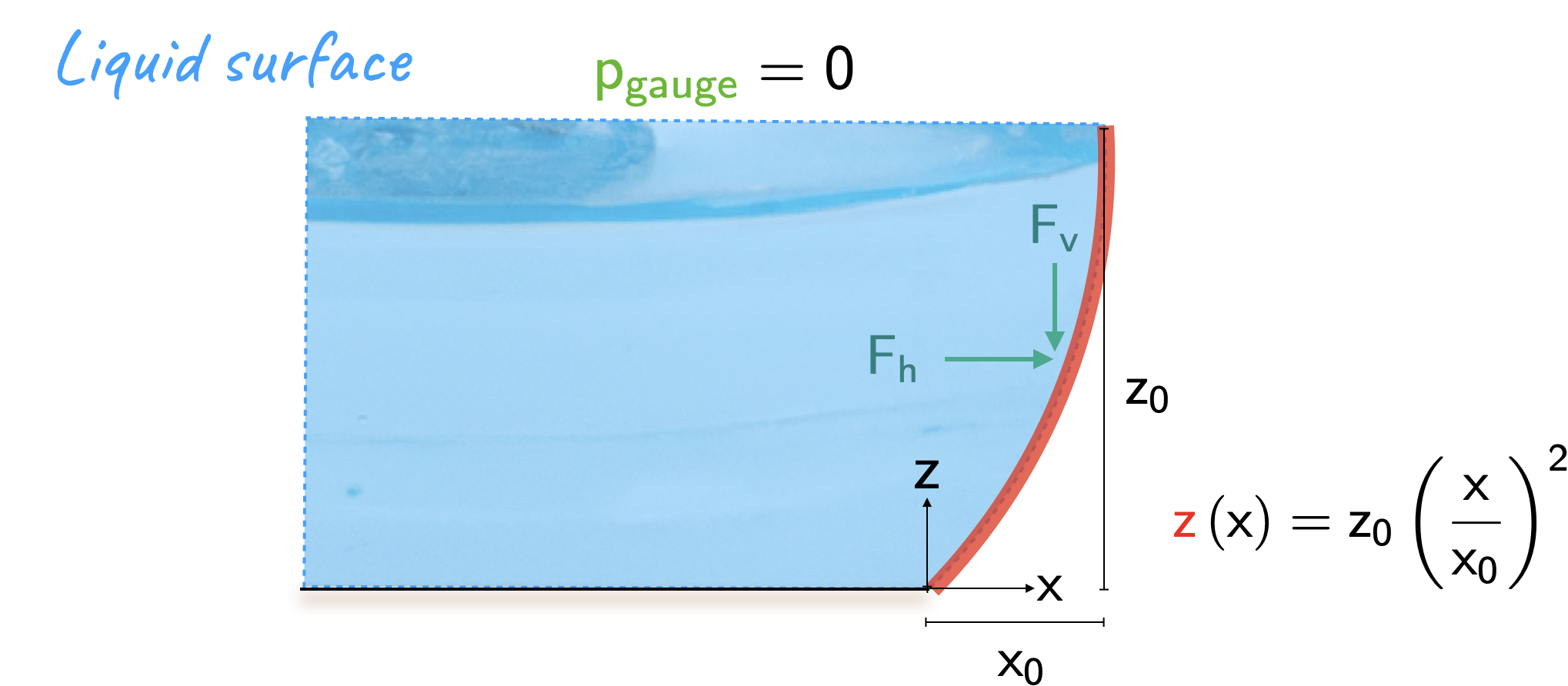orifice orifice

Assuming that the dam is filled with water, and has dimensions \(x_0 = 5 m\) and \(z_0 = 8 m\), calculate the forces \(\require{color}{\color[rgb]{0.064095,0.501831,0.501977}F_v}\) and \(\require{color}{\color[rgb]{0.064095,0.501831,0.501977}F_h}\). The width of the dam (thickness into the page) is given to be \(20 m\) and the density of water in the dam is \(\require{color}{\color[rgb]{0.964810,0.470942,0.057578}\rho} = \require{color}{\color[rgb]{0.964810,0.470942,0.057578}1000 kg / m^3}\).

Solution

As the fluid in the dam is at rest, it is worth noting that the vertical force \(\require{color}{\color[rgb]{0.064095,0.501831,0.501977}F_v}\) corresponds to the weight of the water above, while the horizontal force \(\require{color}{\color[rgb]{0.064095,0.501831,0.501977}F_h}\) is the pressure force across the projected area.

To work out the volume of water above the dam, we integrate the parabola and multiply it by the width (\(w=20 m\)). The first part yields the area

\[ \large \require{color} A = \int_{0}^{x_0} {\color[rgb]{0.986252,0.007236,0.027423}z}\left(x \right)dx = \int_{0}^{x_0} z_0 \left( \frac{x}{x_0} \right)^2 dx \]

\[ \large \require{color} A = \frac{z_0}{x^2_0} \int_{0}^{x_0} x^2 dx = \frac{z_0}{x^2_0} \left[ \frac{x^3}{3} \right]_{0}^{x_0} = \frac{1}{3} x_0 z_0 \]

Note that this is the area underneath the red curve. What we want is the area corresponding to where the water is. This is given by

\[ \large \require{color} A_{water} = x_0 z_0 - \frac{1}{3} x_0 z_0 = \frac{2}{3} x_0 z_0. \]

The volume of water in the parabolic region is thus simply

\[ \large V = \frac{2}{3} x_0 z_0 w. \]

The vertical force may then be written as

\[ \large \require{color}{\color[rgb]{0.064095,0.501831,0.501977}F_v} = {\color[rgb]{0.964810,0.470942,0.057578}\rho} g \frac{2}{3}x_0 z_0 w. \]

For the horizontal force,

\[ \large \require{color}{\color[rgb]{0.064095,0.501831,0.501977}F_h} = w \int_{0}^{z_0} {\color[rgb]{0.964810,0.470942,0.057578}\rho} g {\color[rgb]{0.986252,0.007236,0.027423}z} d{\color[rgb]{0.986252,0.007236,0.027423}z} = w {\color[rgb]{0.964810,0.470942,0.057578}\rho} g \frac{z^2_0}{2} \]

Numerical solutions are given below.
Code 
w = 20
x0 = 5
z0 = 8
rho = 1000
g = 9.8
F_v = rho * g * 2/3 * x0 * z0 * w
print(str(F_v)+' N')
5226666.666666666 N
Code 
F_h = rho * g * w * z0**2 / 2
print(str(F_h)+' N')
6272000.0 N