L17 examples

Problem 1

A mass of air is compressed rapidly within a cylinder by a piston. The initial pressure and temperature are \(\require{color}{\color[rgb]{0.315209,0.728565,0.037706}1 \; bar}\) and \(\require{color}{\color[rgb]{0.164799,0.878862,0.723179}290 \; K}\), and the work input is \(\require{color}{\color[rgb]{0.562040,0.190215,0.568721}100 \; kJ}\) per kilogram of air. Calculate the final pressure and temperature if

1. the compression is reversible
   
2. irreversibilities account for an increase in specific entropy of \(\require{color} {\color[rgb]{0.599997,0.600015,0.600005}0.06 \; kJ/(kg \; K)}\)

Sketch these two cases on a T-s diagram. The specific heat capacity at constant volume for air is \({\color[rgb]{0.878548,0.880173,0.060757}0.72 \; kJ/(kg \; K)}\), the specific heat capacity at constant pressure for air is \({\color[rgb]{0.986252,0.007236,0.027423}1.01 \; kJ/(kg \; K)}\).

Solution

The first in specific quantities is given by

\[ \large \require{color} {\color[rgb]{0.334690,0.296180,0.998454}q} - {\color[rgb]{0.562040,0.190215,0.568721}w} = {\color[rgb]{0.878548,0.880173,0.060757}\Delta u} \]

Now as air is a perfect gas,

\[ \large \require{color} {\color[rgb]{0.878548,0.880173,0.060757}\Delta u} = {\color[rgb]{0.878548,0.880173,0.060757}c}_{{\color[rgb]{0.079785,0.618358,0.483717}V}} {\color[rgb]{0.164799,0.878862,0.723179}\Delta T}. \]

As the process takes place rapidly, we assume that there is no time for heat transfer and therefore it is adiabatic. This implies that \(\require{color}{\color[rgb]{0.334690,0.296180,0.998454}q} = 0\), and thus

\[ \large \require{color} - {\color[rgb]{0.562040,0.190215,0.568721}w} = {\color[rgb]{0.878548,0.880173,0.060757}\Delta u}. \]

Plugging this into the prior equation results in

\[ \large \require{color} {\color[rgb]{0.164799,0.878862,0.723179}\Delta T} = \frac{-{\color[rgb]{0.562040,0.190215,0.568721}w}}{{\color[rgb]{0.878548,0.880173,0.060757}c}_{{\color[rgb]{0.079785,0.618358,0.483717}V}} } = -\frac{-{\color[rgb]{0.562040,0.190215,0.568721}100}}{{\color[rgb]{0.878548,0.880173,0.060757}0.72}} = {\color[rgb]{0.164799,0.878862,0.723179}139 \; K}. \]

Note that there is a negative sign on the work term as the work is done on the system. From this, we arrive at the final temperature of \(\require{color}{\color[rgb]{0.164799,0.878862,0.723179}T_2} = {\color[rgb]{0.164799,0.878862,0.723179}T_1} + {\color[rgb]{0.164799,0.878862,0.723179}\Delta T} = {\color[rgb]{0.164799,0.878862,0.723179}290} + {\color[rgb]{0.164799,0.878862,0.723179}139} = {\color[rgb]{0.164799,0.878862,0.723179}429 \; K}\)

Now we consider the two cases below:

1. From lecture, we learnt that a reversible process that is also adiabatic must be isentropic. This implies we can use the isentropic relations.

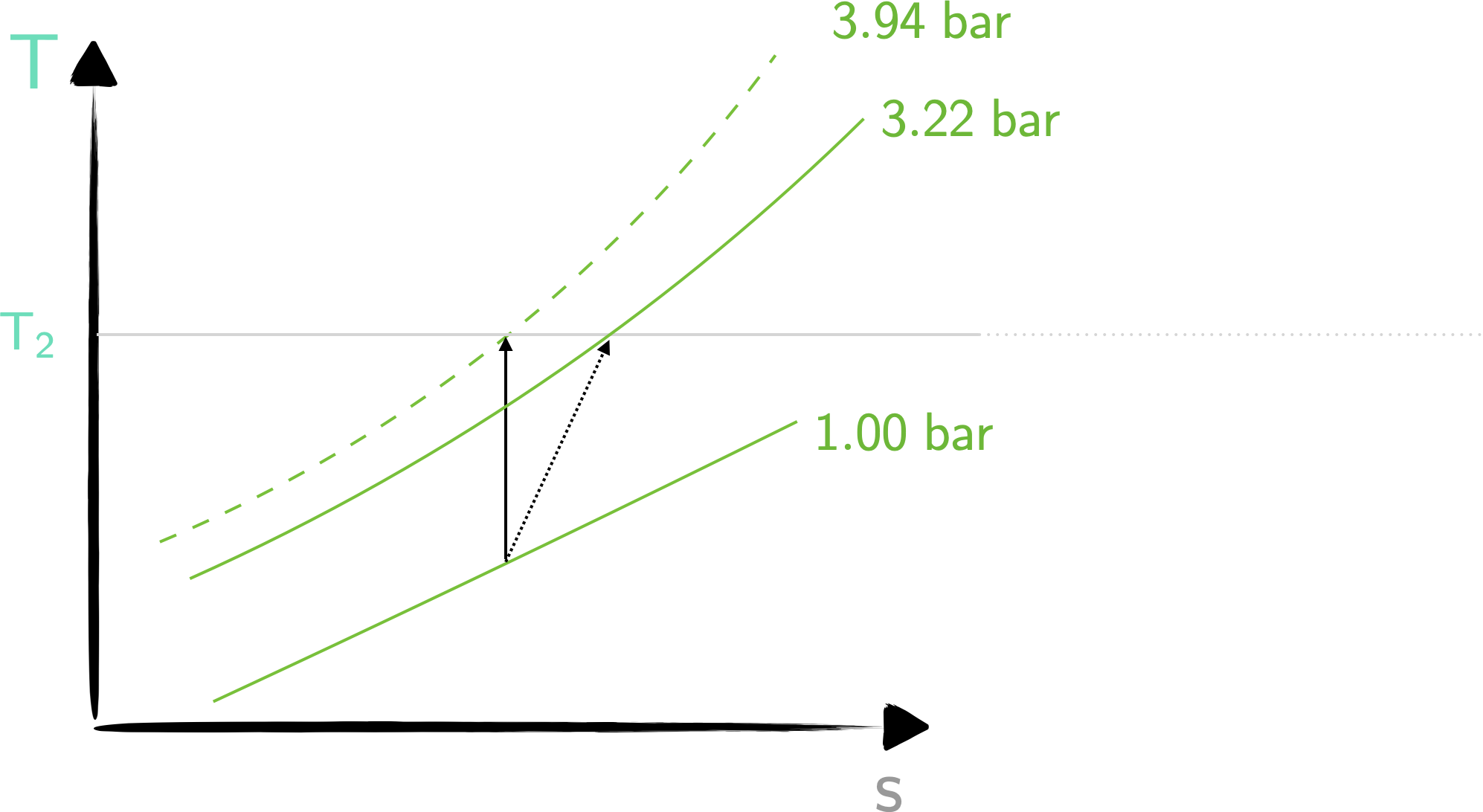
\[ \large \require{color} \left( \frac{{\color[rgb]{0.315209,0.728565,0.037706}p_2}}{{\color[rgb]{0.315209,0.728565,0.037706}p_1}} \right) = \left( \frac{{\color[rgb]{0.164799,0.878862,0.723179}T_2}}{{\color[rgb]{0.164799,0.878862,0.723179}T_1}} \right)^{\frac{\gamma}{\gamma - 1}} = \left( \frac{{\color[rgb]{0.164799,0.878862,0.723179}429}}{{\color[rgb]{0.164799,0.878862,0.723179}290}} \right)^{\frac{1.4}{0.4}} = {\color[rgb]{0.315209,0.728565,0.037706}3.94} \]

Thus \(\require{color}{\color[rgb]{0.315209,0.728565,0.037706}p_2} = {\color[rgb]{0.315209,0.728565,0.037706}3.94 \; bar}\).

2. For an irreversible adiabatic process we need to make use of the Tds relations. Thus we have

\[ \large \require{color} {\color[rgb]{0.599997,0.600015,0.600005}\Delta s} = {\color[rgb]{0.986252,0.007236,0.027423}c}_{\color[rgb]{0.315209,0.728565,0.037706}p} \; ln \left( \frac{{\color[rgb]{0.164799,0.878862,0.723179}T_2}}{{\color[rgb]{0.164799,0.878862,0.723179}T_1}} \right) - R \; ln \left( \frac{{\color[rgb]{0.315209,0.728565,0.037706}p_2}}{{\color[rgb]{0.315209,0.728565,0.037706}p_1}} \right) \]

\[ \large \require{color} \Rightarrow {\color[rgb]{0.599997,0.600015,0.600005} 0.06} = {\color[rgb]{0.986252,0.007236,0.027423}1.01} \; ln \left( \frac{{\color[rgb]{0.164799,0.878862,0.723179}429}}{{\color[rgb]{0.164799,0.878862,0.723179}290}} \right) - 0.287 \; ln \left( \frac{{\color[rgb]{0.315209,0.728565,0.037706}p_2}}{{\color[rgb]{0.315209,0.728565,0.037706}1}} \right) \]

\[ \large \require{color} \Rightarrow {\color[rgb]{0.315209,0.728565,0.037706}p_2} = {\color[rgb]{0.315209,0.728565,0.037706}3.22 \; bar} \]

These two processes are captured in the T-s diagram below.

Problem 2

Consider a closed system that comprises two symmetric chambers. The chamber on the left contains 0.1 kg of air, and the right hand chamber is initially evacuated. The diaphragm is burst and the system comes to equilibrium adiabatically. Find the increase in entropy during the process.

Solution

From the first law,

\[ \large \require{color} {\color[rgb]{0.334690,0.296180,0.998454}Q} - {\color[rgb]{0.562040,0.190215,0.568721}W} = {\color[rgb]{0.878548,0.880173,0.060757}\Delta U } = 0 \]

Treating air as a perfect gas

\[ \large \require{color} {\color[rgb]{0.878548,0.880173,0.060757}\Delta U} = m{\color[rgb]{0.878548,0.880173,0.060757}c}_{{\color[rgb]{0.079785,0.618358,0.483717}V}} {\color[rgb]{0.164799,0.878862,0.723179}\Delta T} = 0 \; \; \; \; \Rightarrow {\color[rgb]{0.164799,0.878862,0.723179}T_2} = {\color[rgb]{0.164799,0.878862,0.723179}T_1} \]

The entropy change for a perfect gas undergoing a general change of state is given by the expressions derived in Lecture 17. As the temperature remains constant, and we know the volume doubles, we choose the expression involving \(\require{color}{\color[rgb]{0.164799,0.878862,0.723179}T}\) and \({\color[rgb]{0.918231,0.469102,0.038229}\nu}\), i.e.,

\[ \large \require{color} {\color[rgb]{0.599997,0.600015,0.600005}\Delta S} = m{\color[rgb]{0.878548,0.880173,0.060757}c}_{{\color[rgb]{0.079785,0.618358,0.483717}V}} ln \left( \frac{{\color[rgb]{0.164799,0.878862,0.723179}T_2}}{{\color[rgb]{0.164799,0.878862,0.723179}T_1}} \right) + m R \; ln \left( \frac{{\color[rgb]{0.079785,0.618358,0.483717}V_2}}{{\color[rgb]{0.079785,0.618358,0.483717}V_1}} \right). \]

Noting that \(\require{color}{\color[rgb]{0.164799,0.878862,0.723179}T_1} = {\color[rgb]{0.164799,0.878862,0.723179}T_2}\) and that \(\require{color}{\color[rgb]{0.079785,0.618358,0.483717}V_2} = 2{\color[rgb]{0.079785,0.618358,0.483717}V_1}\)

\[ \large \require{color} {\color[rgb]{0.599997,0.600015,0.600005}\Delta S} = m R \; ln \left(2 \right) = 0.1 \times 287 \times ln\left(2 \right) = {\color[rgb]{0.599997,0.600015,0.600005}19.9 \; J/K}. \]

Problem 3

A completely evacuated bottle of volume \(\require{color}{\color[rgb]{0.079785,0.618358,0.483717}0.1 \; m^3}\) is to be filled with helium from a main where the pressure is \(\require{color}{\color[rgb]{0.315209,0.728565,0.037706}5 \; bar}\) and the temperature is \(\require{color}{\color[rgb]{0.164799,0.878862,0.723179}300 \; K}\). The bottle is connected as shown, the valve is opened, helium enters the bottle and the valve is shut when the pressure in the bottle is \(\require{color}{\color[rgb]{0.315209,0.728565,0.037706}5 \; bar}\). The bottle is well lagged so there is no heat loss to the surroundings. Using a control volume approach, calculate the final temperature in the bottle and the mass entering. Assume that helium behaves as a perfect gas with \(R = 2.08 \; kJ / (kg K )\) and \(\gamma = 1.67\), and that kinetic and potential energy terms can be ignored.

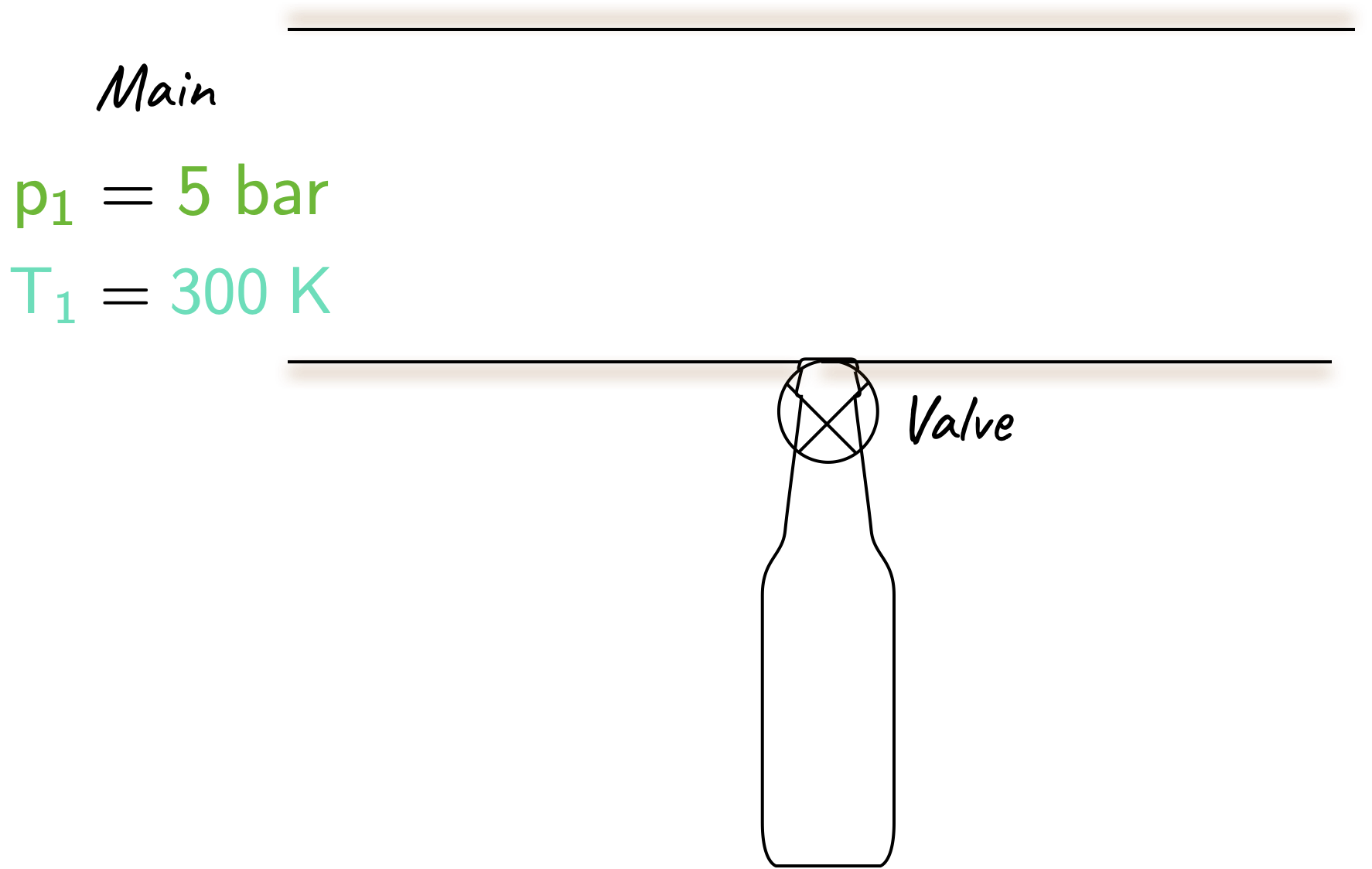
Solution

The solution is given as follows. Neglecting the kinetic and potential energy terms we have the conservation of energy

\[ \large \require{color} {\color[rgb]{0.334690,0.296180,0.998454}\delta Q} - {\color[rgb]{0.562040,0.190215,0.568721}\delta W_{x} }= {\color[rgb]{1.000000,0.869732,0.000000}\delta E}_{cv} - \delta m_i {\color[rgb]{0.986252,0.007236,0.027423}h_i } \]

Recognizing that \(\require{color}{\color[rgb]{0.334690,0.296180,0.998454}\delta Q} = 0\) and \(\require{color}{\color[rgb]{0.562040,0.190215,0.568721}\delta W_{x} } = 0\), we have

\[ \large \require{color} {\color[rgb]{1.000000,0.869732,0.000000}\delta E}_{cv} = \delta m_i {\color[rgb]{0.986252,0.007236,0.027423}h_i } \]

As \(\require{color}{\color[rgb]{0.986252,0.007236,0.027423}h_i }\) is a constant in the main section over the whole process we get

\[ \large \require{color} m_i \left( {\color[rgb]{0.878548,0.880173,0.060757}c}_{\color[rgb]{0.079785,0.618358,0.483717}V} {\color[rgb]{0.164799,0.878862,0.723179}T_2} + {\color[rgb]{0.878548,0.880173,0.060757}u_0} \right) = m_i \left( {\color[rgb]{0.986252,0.007236,0.027423}c}_{\color[rgb]{0.315209,0.728565,0.037706}p} {\color[rgb]{0.164799,0.878862,0.723179}T_i} + {\color[rgb]{0.878548,0.880173,0.060757}u_0} \right) \]

where \(\require{color}{\color[rgb]{0.878548,0.880173,0.060757}u_0}\) is an arbitrary datum. The above results in

\[ \large \require{color} {\color[rgb]{0.164799,0.878862,0.723179}T_2} = \frac{{\color[rgb]{0.986252,0.007236,0.027423}c}_{\color[rgb]{0.315209,0.728565,0.037706}p}}{{\color[rgb]{0.878548,0.880173,0.060757}c}_{\color[rgb]{0.079785,0.618358,0.483717}V}} {\color[rgb]{0.164799,0.878862,0.723179}T_i} = \gamma {\color[rgb]{0.164799,0.878862,0.723179}T_i} = 1.67 \times {\color[rgb]{0.164799,0.878862,0.723179}300} = {\color[rgb]{0.164799,0.878862,0.723179}501 \; K} \]

From the ideal gas relation we have

\[ \large \require{color} {\color[rgb]{0.315209,0.728565,0.037706}p_2} {\color[rgb]{0.079785,0.618358,0.483717}V} = m_i R {\color[rgb]{0.164799,0.878862,0.723179}T_2} \Rightarrow m_i = \frac{{\color[rgb]{0.315209,0.728565,0.037706}p_2} {\color[rgb]{0.079785,0.618358,0.483717}V}}{R {\color[rgb]{0.164799,0.878862,0.723179}T_2}} = \frac{{\color[rgb]{0.315209,0.728565,0.037706}5 \times 10^5} \times {\color[rgb]{0.079785,0.618358,0.483717}0.1}}{2080 \times {\color[rgb]{0.164799,0.878862,0.723179}501}} = 0.048 \; kg \]

The use of \(\require{color}{\color[rgb]{0.878548,0.880173,0.060757}u_0}\) arises because only changes in internal energy can be calculated, so for our general case we take it to be an arbitrary reference datum.

Note that the negation of kinetic energy at the entry to the bottle may seem rather dubious; velocities are infact very high here. However, the helium entering at this point originally came from upstream in the main where the velocities are low, and it may be shown that the value of \(\require{color}{\color[rgb]{0.986252,0.007236,0.027423}h_i}\) used above is correct.